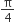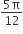Clocks
Sponsor Area
A clock gains 15 minutes per day. If it is set right at 12 noon, the time it shows at 4 AM is
-
4.20 AM
-
4.30 AM
-
4.02 AM
-
4.10 AM
D.
4.10 AM
Total hours between 12 p.m. and 4 a.m. = 16 hours.
According to the question,
The clock is gaining in 24 hours = 15 min
In 1 hour, the clock will gain = 
In 16 hours, the clock will gain = 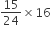
= 10 min
Therefore, required time = 4.10 a.m.
Sponsor Area
A wall clock gains 2 minutes in 12 hours, while a table clock loses 2 minutes every 36 hours. Both are set right at 12 noon on Tuesday. The correct time when both show the same time next would be
-
12.30 at night, after 130 days
-
12 noon, after 135 days
-
1.30 at night, after 130 days
-
12 midnight, after 135 days
B.
12 noon, after 135 days
A wall clock gains 2 min in every 12 hours, so it would gain 6 min in 36 hours.
and table clock losses two minutes in every 36 hours.
So, in every 36 hours they difference between them is 8 min.
They will be at the same time when the difference between them is 12 hours.
Hence, 8 min = 36 hours
So, 1 min difference = 
Or 12 x 60 min difference in 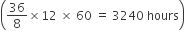
or 3240 hours is 135 days.
Hence both clocks will show same time at 12 noon after 135 days.
If a clock strikes appropriate number of times at each hour, how many times will it strike a day?
-
300
-
156
-
68
-
78
B.
156
Clock will strike 1 time at 1, 2 times at 2, 3 times at 3, and so on up through 12 times at 12.
This makes 1+2+3+4+5+6+7+8+9+10+11+12=78 times every 12 hours.
i.e. it strikes (78 x 2) = 156 times in 24 hours.
The circular measure of the included angle formed by the hour hand and minute hand of a clock at 3 p.m. will be
D.
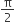
Required angle:
Sponsor Area
Mock Test Series
Mock Test Series