Find the greatest number which will exactly divide 200 and 320.
-
10
-
20
-
16
-
40
D.
40
Required number = HCF of 200 and 320 = 40
Sponsor Area
Find the greatest number which will exactly divide 200 and 320.
10
20
16
40
D.
40
Required number = HCF of 200 and 320 = 40
Sponsor Area
Find the least number which when divided separately by 15, 20, 36 and 48 leaves 3 as remainder in each case.
243
483
723
D.
723
Required number = (L.C.M. of 15, 20, 36 and 48) + 3
= 720 + 3 = 723
H.C.F. of 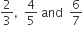 is
is




B.

H.C.F. of 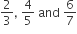
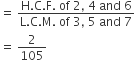
If the L.C.M. and H.C.F. of two expressions are (x2 + 6x + 8) (x + 1) and (x + 1) respectively and one of the expressions is x2 + 3x + 2, find the other.
x2 + 5x + 4
x2 - 5x + 4
x2 + 4x + 5
x2 - 4x + 5
A.
x2 + 5x + 4
x2 + 6x + 8 = x2 + 4x + 2x +8 = x(x + 4) + 2(x + 4) = (x + 4) (x + 2)
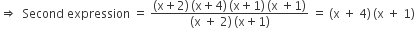
If the students of 9th class are arranged in a row of 6, 8, 12 or 16, no student is left behind. Then the possible number of students in the class is
60
72
80
96
D.
96
Required number of students = L.C.M. of 6, 8, 12 and 16 is 96.
Sponsor Area
Mock Test Series