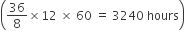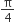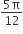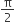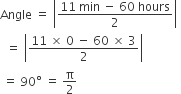+91-8076753736 [email protected]
logo
logo

Clocks

Sponsor Area

Question
SSCCGLENQA12042287
Wired Faculty App

A clock gains 15 minutes per day. If it is set right at 12 noon, the time it shows at 4 AM is

  • 4.20 AM

  • 4.30 AM

  • 4.02 AM

  • 4.10 AM

Solution

D.

4.10 AM

Total hours between 12 p.m. and 4 a.m. = 16 hours.
According to the question,
The clock is gaining in 24 hours  = 15 min
In 1 hour, the clock will gain = 15 over 24 min
 In 16 hours, the clock will gain  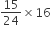= 15 over 24 cross times 16
                                               = 10 min
Therefore, required time = 4.10 a.m.

Sponsor Area

Question
SSCCGLENQA12043036
Wired Faculty App

A wall clock gains 2 minutes in 12 hours, while a table clock loses 2 minutes every 36 hours. Both are set right at 12 noon on Tuesday. The correct time when both show the same time next would be

  • 12.30 at night, after 130 days

  • 12 noon, after 135 days

  • 1.30 at night, after 130 days

  • 12 midnight, after 135 days

Solution

B.

12 noon, after 135 days

A wall clock gains 2 min in every 12 hours, so it would gain 6 min in 36 hours.
and table clock losses two minutes in every 36 hours.
So, in every 36 hours they difference between them is 8 min.
They will be at the same time when the difference between them is 12 hours.
Hence, 8  min = 36 hours
So, 1 min difference = 36 over 8
Or 12 x 60 min difference in open parentheses 36 over 8 cross times 12 space cross times space 60 space equals space 3240 space hours close parentheses
or  3240 hours is 135 days.
Hence both clocks will show same time at 12 noon after 135 days.

Question
SSCCGLENQA12042821
Wired Faculty App

If a clock strikes appropriate number of times at each hour, how many times will it strike a day?

  • 300

  • 156

  • 68

  • 78

Solution

B.

156

Clock will strike 1 time at 1, 2 times at 2, 3 times at 3, and so on up through 12 times at 12.
This makes 1+2+3+4+5+6+7+8+9+10+11+12=78 times every 12 hours. 
i.e. it strikes (78 x 2)  = 156 times in 24 hours.

Question
SSCCGLENQA12043682
Wired Faculty App

The circular measure of the included angle formed by the hour hand and minute hand of a clock at 3 p.m. will be

  • straight pi over 4

  • straight pi over 3

  • fraction numerator 5 straight pi over denominator 12 end fraction

  • straight pi over 2

Solution

D.

straight pi over 2

Required angle:
   Angle space equals space open vertical bar fraction numerator 11 space min space minus space 60 space hours over denominator 2 end fraction close vertical bar space space space equals space open vertical bar fraction numerator 11 space cross times space 0 space minus space 60 space cross times space 3 over denominator 2 end fraction close vertical bar space equals space 90 degree space equals space straight pi over 2

Sponsor Area

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation