Oscillations
Sponsor Area
are functions of time, then the value of t at which they are orthogonal to each other
-
-
-
-
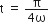
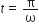
t = 0
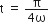
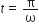
t = 0
C.
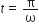
For a perpendicular vector, we have A. B = 0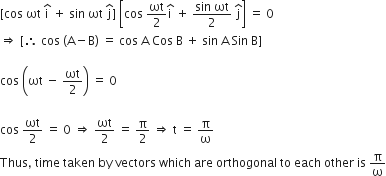 
Sponsor Area
A block of mass M is attached to the lower end of a vertical strong. The string is hung from a ceiling and has to force constant value k. The mass is released from rest with the spring initially unstretched. The maximum extension produced in the length of the spring will be
-
Mg/k
-
2Mg//k
-
4 Mg/ k
-
Mg/2k
B.
2Mg//k
Use of the law of conservation of energy. Let x be the extension in the spring.
Applying conservation of energy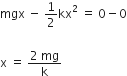
A mass of 2.0 Kg is put on a flat pan attached to a vertical spring fixed on the ground as shown in the figure. The mass of the spring and the pan is negligible. When pressed slightly and released the mass executes a simple harmonic motion. The spring constant is 200 N/m. What should be the minimum amplitude of the motion, so that the mass gets detached from the pan?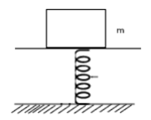
Take g = `10 m/s2
-
8.0 cm
-
10.0 cm
-
any value less than 12.0 cm
-
4.0
B.
10.0 cm
Let he minimum amplitue of SHM is a.
Restoring force on spring
F = ka
Restoring force is balanced by weight mg of block. For mass to execute simple harmonic motion of amplitude a.
ka = mg
a = mg/k
Here, m =2 kg, k = 200 N/m, g = 10 m/s2
therefore, a = 2 x 10 / 200 = 10/100 m.
10 cm
A particle executes linear simple harmonic motion with an amplitude of 3 cm. When the particle is at 2 cm from the mean position, the magnitude of its velocity is equal to that of its acceleration. Then its time period in seconds is
C.
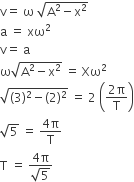
A particle executes simple harmonic oscillation with an amplitude a. The period of oscillation is T. The minimum time taken by the particle to travel half of the amplitude from the equilibrium position is:
-
T/4
-
T/8
-
T/12
-
T/2
C.
T/12
Let displacement equation of particle executing SHM is
y = a sin ωt
As particle travels half of the amplitude from the equilibrium position, so
y= a/2
therefore,
Hence, the particle travels half of the amplitude from the equilibrium in T/12 sec.
Sponsor Area
Mock Test Series
Mock Test Series