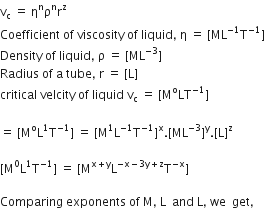+91-8076753736 support@wiredfaculty.com
Wired Faculty Logo
Wired Faculty Logo Wired Faculty

Mechanical Properties of Fluids

Sponsor Area

Question
CBSEENPH11020579
Wired Faculty App

A certain number of spherical drops of a liquid of radius r coalesce to form a single drop of radius R and volume V. If T is the surface tension of the liquid, then

  • Energy = 4VT open parentheses 1 over straight r minus 1 over straight R close parentheses is released.

  • Energy = 3VTopen parentheses 1 over straight r plus 1 over R close parentheses is absorbed

  • Energy = 3 VT 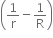open parentheses 1 over straight r minus 1 over straight R close parentheses is released

  • Energy is neither absorbed nor released.

Solution

C.

Energy = 3 VT 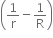open parentheses 1 over straight r minus 1 over straight R close parentheses is released

If the surface area changes, it will change the surface energy also.
When the surface area decreases, it means energy is released ad vice-versa.
Change in surface energy is increment straight A space straight x space straight T   ... (i)
Let, there be n number of drops initially.
So, increment straight A space equals space 4 πR squared space minus space straight n space left parenthesis 4 πr squared right parenthesis       ... (ii)
Volume is constant.
So, 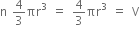straight n space 4 over 3 πr cubed space equals space 4 over 3 πr cubed space equals space straight V         ... (iii)
From equations (ii) and (iii), we have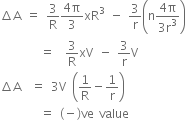
increment straight A space equals space 3 over straight R fraction numerator 4 straight pi over denominator 3 end fraction xR cubed space minus space 3 over straight r open parentheses straight n fraction numerator 4 straight pi over denominator 3 straight r cubed end fraction close parentheses space space space space space space space space equals space space 3 over straight R xV space minus space 3 over straight r straight V increment straight A space space equals space 3 straight V space open parentheses 1 over straight R minus 1 over straight r close parentheses space space space space space space space space equals space left parenthesis negative right parenthesis ve space value
Since, R > r, incrementA is negative.
That is, the surface area is decreased.
Hence, energy must be released.
Energy released = increment straight A space straight x space straight T space equals space minus 3 VT open parentheses 1 over straight r minus 1 over straight R close parentheses
In the above expression, (-)ve sign shows that amount of energy is released.

Sponsor Area

Question
CBSEENPH11020810
Wired Faculty App

A U tube with both ends open to the atmosphere is partially filled with water. Oil, which is immiscible with water, is poured into one side until it stands at a distance of 10 mm above the water level on the other side. Meanwhile, the water rises by 65 mm from its original level (see diagram). The density of the oil is

  • 650 kg m–3

  • 425 kg m–3

  • 800 kg m–3

  • 928 kg m–3

Solution

D.

928 kg m–3

hoil ρoil g = hwater ρwater g
140 × ρoil= 130 × ρwater
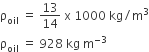
straight rho subscript oil space equals space 13 over 14 space straight x space 1000 space kg divided by straight m cubed straight rho subscript oil space equals space 928 space kg space straight m to the power of negative 3 end exponent

Question
CBSEENPH11020643
Wired Faculty App

If dimensions of critical velocity vc of a liquid flowing through  a tube are expressed as left square bracket straight eta to the power of straight x space straight rho to the power of straight y space straight r to the power of straight z right square bracket comma space where space straight eta comma space straight rho space and space straight r are the coefficient of viscosity of liquid, density of liquid and radius of the tube respectively, then the values of x, y and z are given by

  • 1,-1,-1

  • -1,-1,1

  • -1,-1,-1

  • 1,1,1

Solution

A.

1,-1,-1

According to the principle of homogeneity of dimension states that, a physical quantity equation will be dimensionally correct if the dimension of all the terms occurring on both sides of the equations is same.
Given critical velocity of liquid flowing through a tube are expressed as
straight v subscript straight c space equals space straight eta to the power of straight n straight rho to the power of straight n straight r to the power of straight z Coefficient space of space viscosity space of space liquid comma space straight eta space equals space left square bracket ML to the power of negative 1 end exponent straight T to the power of negative 1 end exponent right square bracket Density space of space liquid comma space straight rho space equals space left square bracket ML to the power of negative 3 end exponent right square bracket Radius space of space straight a space tube comma space straight r space equals space left square bracket straight L right square bracket critical space velcity space of space liquid space straight v subscript straight c space equals space left square bracket straight M to the power of straight o LT to the power of negative 1 end exponent right square bracket equals space left square bracket straight M to the power of straight o straight L to the power of 1 straight T to the power of negative 1 end exponent right square bracket space equals space left square bracket straight M to the power of 1 straight L to the power of negative 1 end exponent straight T to the power of negative 1 end exponent right square bracket to the power of straight x. left square bracket ML to the power of negative 3 end exponent right square bracket to the power of straight y. left square bracket straight L right square bracket to the power of straight z left square bracket straight M to the power of 0 straight L to the power of 1 straight T to the power of negative 1 end exponent right square bracket space equals space left square bracket straight M to the power of straight x plus straight y end exponent straight L to the power of negative straight x minus 3 straight y plus straight z end exponent straight T to the power of negative straight x end exponent right square bracket Comparing space exponents space of space straight M comma space straight L space space and space straight L comma space we space space get comma
x+ y = 0, - x-3y+z = 1, -x = -1
z = -11 x = 1, y = -1

Question
CBSEENPH11020612
Wired Faculty App

The wettability of a surface by a liquid depends primarily on

  • viscosity

  • surface tension

  • density

  • angle of contact between the surface and the liquid

Solution

D.

angle of contact between the surface and the liquid

The value of angle of contact determines whether a liquid will spread on the surface or not.

Question
CBSEENPH12039767
Wired Faculty App

The wind with speed 40 m/s blows parallel to the roof of a house. The area of the roof is 250m2. Assuming that the pressure inside the house is atmospheric pressure, the force exerted by the wind on the roof and the direction of the force will be( pair = 1.2 kg/m3)

  • 4.8 x 105 N, downwards

  • 4.8 x105 N , upwards

  • 2.4 x 105 N , upwards

  • 2.4 x 105 N , upwards

Solution

C.

2.4 x 105 N , upwards

From Bernoulli's theorem
straight p subscript 1 space plus 1 half ρv subscript 1 superscript 2 space equals space straight p subscript 2 plus 1 half ρv subscript 2 superscript 2
Where p1,p2 are pressure inside and outside the roof and v1, v2 are velocities of the wind inside and outside the roof. Neglect the Width of the roof.
Pressure difference is 
p1 -p2 =straight p subscript 1 space minus straight p subscript 2 space equals space 1 half straight rho space left parenthesis straight v subscript 2 superscript 2 minus straight v subscript 1 superscript 2 right parenthesis equals space 1 half space straight x space 1.2 space left parenthesis 40 squared minus 0 right parenthesis space equals space 960 space straight N divided by straight m squared
Force acting on the roof is given by
F= (p1 -p2) A = 960 x 250
 = 24 x 104 N  = 24 x 105 N
As the pressure inside the roof is more than outside to it. So the force will act in the upward direction i.e. F = 24 x 105 N -upward.

Sponsor Area

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

4