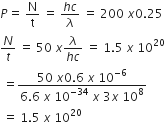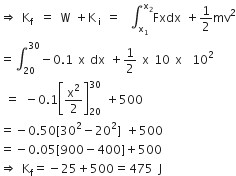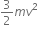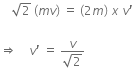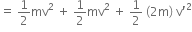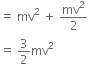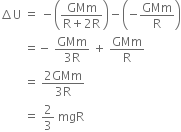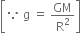+91-8076753736 support@wiredfaculty.com
Wired Faculty Logo
Wired Faculty Logo Wired Faculty

Work, Energy and Power

Sponsor Area

Question
CBSEENPH11020570
Wired Faculty App

A 200 W sodium street lamp emits yellow light of wavelength 0.6 um. Assuming it to be 25% efficient in converting electrical energy to light, the number of photons of yellow light it emits per second is

  • 1.5 x 1020

  • 6 x 1018

  • 62 x 1020

  • 3 x1019

Solution

A.

1.5 x 1020

 Efficient power P= 
P equals space straight N over straight t space equals space fraction numerator h c over denominator lambda end fraction space equals space 200 space x 0.25 N over t space equals space 50 space x fraction numerator lambda over denominator h c end fraction space equals space 1.5 space x space 10 to the power of 20 space equals fraction numerator 50 space x 0.6 space x space 10 to the power of negative 6 end exponent over denominator 6.6 space x space 10 to the power of negative 34 end exponent space x space 3 x space 10 to the power of 8 end fraction space equals space 1.5 space x space 10 to the power of 20

Sponsor Area

Question
CBSEENPH11020642
Wired Faculty App

A ball is thrown vertically downwards from a height of 20m with an initial velocity vo, It collides with the ground, loses 50% of its energy in collision and rebounds to the same height. The initial velocity vo is,

(Take g = 10 ms-2)

  • 14 ms-1

  • 20 ms-1

  • 28 ms-1

  • 10 ms-1

Solution

B.

20 ms-1

Suppose a ball rebounds with speed v,

straight v space equals space square root of 2 gh space end root space equals space square root of 2 space straight x space 10 space straight x space 20 space end root space equals space 20 space straight m divided by straight s Energy space of space straight a space ball space just space after space rebound comma straight E space equals space 1 half space mv squared space equals space 200 space straight m As comma space 50 space percent sign space of space energy space loses space in space collision space means space just space before space collision space energy space 400 space straight m. According space to space law space of space conservation space of space energy comma space we space have 1 half space mv subscript 0 superscript 2 space space plus space mgh space equals space 400 space straight m rightwards double arrow space 1 half mv subscript 0 superscript 2 space plus space straight m space straight x space 10 space straight x space 20 space equals space 400 space straight m space rightwards double arrow space straight v subscript straight o space equals space 20 space straight m divided by straight s

Question
CBSEENPH11020528
Wired Faculty App

A block of mass 10 kg, moving in the x-direction with a constant speed of 10 ms-1 , is subjected to a retarding force F= 0.1x J/m during its travel from x = 20 m to 30 m. Its final KE will be

  • 475 J

  • 450 J

  • 275 J

  • 250 J 

Solution

A.

475 J

From work energy theorem
work done = change in KE
⇒ W = Kf -Ki
rightwards double arrow space straight K subscript straight f end subscript space equals space straight W space plus straight K subscript straight i space end subscript equals space integral subscript straight x subscript 1 end subscript superscript straight x subscript 2 end superscript Fxdx space plus 1 half mv squared equals integral subscript 20 superscript 30 minus 0.1 space straight x space dx space plus 1 half space straight x space 10 space straight x space space 10 squared space equals space minus 0.1 open square brackets straight x squared over 2 close square brackets subscript 20 superscript 30 space plus 500 equals negative 0.50 left square bracket 30 squared minus 20 squared right square bracket space plus 500 equals negative 0.05 left square bracket 900 minus 400 right square bracket plus 500 rightwards double arrow space straight K subscript straight f equals negative 25 plus 500 equals 475 space straight J

Question
CBSEENPH11020569
Wired Faculty App

A body of mass (4m) is lying in x-y plane at rest. It suddenly explodes into three pieces. Two pieces each of mass m move perpendicular to each other with equal speed (v). The total kinetic energy generated due to explosion is,

  • mv2

  • 3 over 2 m v squared

  • 2mv2

  • 4 mv2

Solution

B.

3 over 2 m v squared
As per the question, the third part of mass 2m will move because the total momentum of the system after explosion must remain zero.
Let the velocity of the third part be v'.
According to the law of conservation of momentum,
space space space space square root of 2 space left parenthesis m v right parenthesis space equals space left parenthesis 2 m right parenthesis space x space v apostrophe rightwards double arrow space space space space v apostrophe space equals space fraction numerator v over denominator square root of 2 end fraction
Total kinetic energy generated by the explosion,
equals space 1 half mv squared space plus space 1 half mv squared space plus space 1 half space left parenthesis 2 straight m right parenthesis space straight v apostrophe squared
equals space mv squared space plus space mv squared over 2 equals space 3 over 2 mv squared

Question
CBSEENPH12039774
Wired Faculty App

A body of mass m taken from the earth's surface to the height equal to twice the radius (R) of the earth. The change in potential energy of the body will be

  • mg2R

  • 2/3 mgR

  • 3 mgR

  • 1/3 mgR

Solution

B.

2/3 mgR

Change in potential energy,
increment straight U space equals space minus open parentheses fraction numerator GMm over denominator straight R plus 2 straight R end fraction close parentheses minus open parentheses negative GMm over straight R close parentheses space space space space space space space space equals negative space fraction numerator GMm over denominator 3 straight R end fraction space plus space GMm over straight R space space space space space space space space equals space fraction numerator 2 GMm over denominator 3 straight R end fraction space space space space space space space space equals space 2 over 3 space mgR open square brackets because space straight g space equals space GM over straight R squared close square brackets

Sponsor Area

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

2