Moving Charges And Magnetism
Sponsor Area
A charged oil drop is suspended in a uniform field of 3 × 104 V/m so that it neither falls nor rises. The charge on the drop will be (take the mass of the charge = 9.9 × 10−15 kg and g = 10 m/s2 )
-
3.3 × 10−18 C
-
3.2 × 10−18 C
-
1.6 × 10−18 C
-
4.8 × 10−18 C
A.
3.3 × 10−18 C
In steady state, electric force on drop = weight of drop
∴ qE = mg
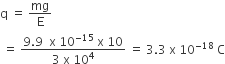
Sponsor Area
A charged particle of mass m and charge q travels on a circular path of radius r that is perpendicular to a magnetic field B. The time taken by the particle to complete one revolution is
D.
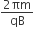
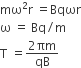
A current I ampere flows along an infinitely long straight thin-walled tube, then the magnetic induction at any point inside the tube is
-
infinite
-
zero
-
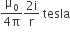
-

B.
zero
Let R be the radius of a long thin cylindrical shell. To calculate the magnetic induction at a distance r (r < R) from the axis of cylinder, a circular shell of radius r is shown: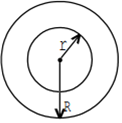
Since no current is enclosed in the circle so, from Ampere's circuital law, magnetic induction is zero at every point of the circle. Hence, the magnetic induction at any point inside the infinitely long straight thin-walled tube (cylindrical) is zero.
A current loop ABCD is held fixed on the plane of the paper as shown in the figure. The arcs BC (radius = b) and DA (radius = a) of the loop are joined by two straight wires AB andCD. A steady current I is flowing in the loop. Angle made by AB and CD at the origin O is 30º. Another straight thin wire with steady current I1 flowing out of the plane of the paper is kept at the origin.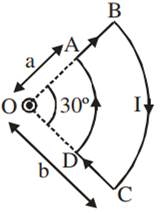
The magnitude of the magnetic field (2) due to the loop ABCD at the origin (O) is
-
zero
-
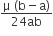
-
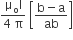
-
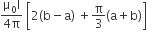
B.
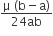
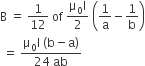
A current loop ABCD is held fixed on the plane of the paper as shown in the figure. The arcs BC (radius = b) and DA (radius = a) of the loop are joined by two straight wires AB andCD. A steady current I is flowing in the loop. Angle made by AB and CD at the origin O is 30º. Another straight thin wire with steady current I1 flowing out of the plane of the paper is kept at the origin.
Due to the presence of the current I1 at the origin
The magnitude of the magnetic field (2) due to the loop ABCD at the origin (O) is
-
The forces on AB and DC are zero
-
The forces on AD and BC are zero
-
The magnitude of the net force on the loop is given by
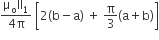
-
The magnitude of the net force on the loop is given by
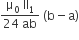
B.
The forces on AD and BC are zero
The forces on AD and BC are zero because magnetic field due to a straight wire on AD and BC is parallel to elementary length of the loop.
Sponsor Area
Mock Test Series
Mock Test Series








