Electrostatic Potential And Capacitance
Sponsor Area
A battery is used to charge a parallel plate capacitor till the potential difference between the plates becomes equal to the electromotive force of the battery. The ratio of the energy stored in the capacitor and the work done by the battery will be
-
1
-
2
-
1/4
-
1/2
D.
1/2
Sponsor Area
A capacitance of 2 μF is required in an electrical circuit across a potential difference of 1.0 kV. A large number of 1 μF capacitors are available which can withstand a potential difference of not more than 300 V. The minimum number of capacitors required to achieve this is :
-
24
-
32
-
2
-
16
B.
32
To hold 1 KV potential difference minimum four capacitors are required in series
⇒ C1 = 1/4
for one series.
So for Ceq to be 2μF, 8 parallel combinations are required.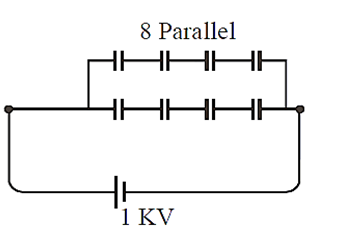
⇒ Minimum no. of capacitors = 8 × 4 = 32
A charge Q is placed at each of the opposite corners of a square. A charge q is placed at each of the other tow corners. If the net electrical force on Q is zero, then Q/q equals
-
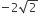
-
1
-
-1
-
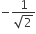
A.
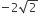
Three forces F41, F42 and f43 acting on Q are shown Resultant of F41 + F43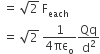
Resultant on Q becomes zero only when ‘q’ charges are of negative nature.
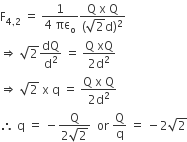
A combination of capacitors is set up as shown in the figure. The magnitude of the electric field, due to a point charge Q (having a charge equal to the sum of the charges on the 4 µF and 9 µF capacitors), at a point distant 30 m from it, would equal: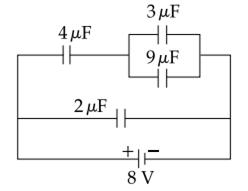
-
240N/C
-
360N/C
-
420N/C
-
480N/C
C.
420N/C
Resultant circuit,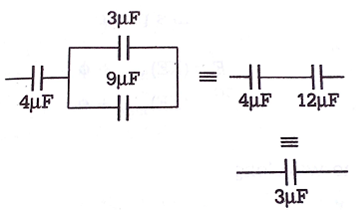
As, charge on 3μF = 3μF x 8V = 24μC
Charge on 3μF = 3μF x 2V = 18 μC
charge on 4μF +Charge on 9μF
= (24 + 18)μC = 42μC
therefore,
Electric field at a point distant 30 m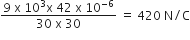
A fully charged capacitor C with initial charge q0 is connected to a coil of self inductance L at t = 0. The time at which the energy is stored equally between the electric and the magnetic fields is
A.
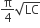
As initially, charge is maximum
∴ q = qocos ωt
Current, 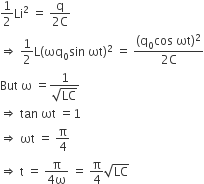
Sponsor Area
Mock Test Series
Mock Test Series








