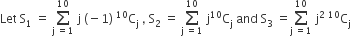+91-8076753736 support@wiredfaculty.com
Wired Faculty Logo
Wired Faculty Logo Wired Faculty

Sequences And Series

Sponsor Area

Question
CBSEENMA11015537
Wired Faculty App

Let space straight S subscript 1 space equals space sum from straight j space equals 1 to 10 of space straight j space left parenthesis negative 1 right parenthesis space to the power of 10 straight C subscript straight j space comma space straight S subscript 2 space equals space sum from straight j space equals 1 to 10 of space straight j to the power of 10 straight C subscript straight j space and space straight S subscript 3 space equals sum from straight j space equals 1 to 10 of space straight j squared space to the power of 10 straight C subscript straight j

Statement-1: S3 = 55 × 29.
Statement-2: S1 = 90 × 28 and S2 = 10 × 28.

  • Statement-1 is true, Statement-2 is true; Statement-2 is a correct explanation for Statement-1.

  • Statement-1 is true, Statement-2 is true; statement-2 is not a correct explanation for Statement-1. 

  • Statement-1 is true, Statement-2 is false.

  • Statement-1 is false, Statement-2 is true.

Solution

C.

Statement-1 is true, Statement-2 is false.

WiredFaculty

Sponsor Area

Question
CBSEENMA11015521
Wired Faculty App

A man saves Rs. 200 in each of the first three months of his service. In each of the subsequent months his saving increases by Rs. 40 more than the saving of immediately previous month. His total saving from the start of service will be Rs. 11040 after

  • 18 Months

  • 19 Months

  • 20 Months

  • 21 Months

Solution

D.

21 Months

a = Rs. 200
d = Rs. 40
savings in first two months = Rs. 400
remained savings = 200 + 240 + 280 + ..... upto n terms =
n/2[400 + (n -1)40] = 11040 - 400
200n + 20n2 - 20n = 10640
20n2 + 180 n - 10640 = 0
n2 + 9n - 532 = 0
(n + 28) (n - 19) = 0
n = 19
∴ no. of months = 19 + 2 = 21

Question
CBSEENMA11015530
Wired Faculty App

A person is to count 4500 currency notes. Let a denote the number of notes he counts in the nth minute. If a1 = a2 = ... = a10 = 150 and a10, a11, ...are in an AP with common difference -2, then the time taken by him to count all notes is

  • 24 min

  • 34 min

  • 125 min

  • 135 min

Solution

B.

34 min

Let the first term of an AP be a and common difference be d and number of terms be n, then 
tn = a + (n-1)d and Sn = n/2 [ 2a + (n-1)d]
Number of notes that the person counts in 10 min = 10 x 150 = 1500
Since a10, a11, a12, .... are in AP in with common difference -2
Let n be the time has taken to count remaining 3000 notes than
n/2[2 x 148 + (n-1) x -2] = 3000
⇒ n2-149n +3000 = 0 
⇒ (n-24)n-125) = 0 
n = 24, 125
Then, the total time taken by the person to count all notes = 10 +24 = 34 min
n = 125 is discarded as putting n = 125
an = 148 + (125-1)(-2)
= 148 - 124 x 2 = 148-248 = -100
⇒ Number of notes cannot be negative.

Question
CBSEENMA11015541
Wired Faculty App

For any three positive real numbers a, b and c, (25a2 + b2) + 25(c2 – 3ac) = 15b(3a + c), Then

  • b , c and a are in G.P

  • b, c and a are in A.P

  • a, b and c are in A.P

  • a, b and c are in G.P

Solution

B.

b, c and a are in A.P

225a2 + 9b2 + 25c2 – 75ac – 45ab – 15bc = 0
(15a)2 + (3b)2 + (5c)2 – (15a)(3b) – (3b)(5c) – (15a) (5c) = 0
1/2[(15a – 3b)2 + (3b – 5c)2 + (5c – 15a)2] = 0
15a = 3b , 3b = 5c , 5c = 15a
5a = b , 3b = 5c , c = 3a
a/1 = b/5 = c/3
a = λ, b = 5λ, c = 3λ
a, c, b are in AP

Question
CBSEENMA11015640
Wired Faculty App

If straight x space equals space sum from straight n equals space 0 to infinity of straight a to the power of straight n comma space straight y space equals space sum from straight n equals 0 to infinity of straight b to the power of straight n comma space sum from straight n equals 0 to infinity of straight c to the power of straight n where a, b, c are in A.P. and |a| < 1, |b|<1, |c|< 1, then x, y, z are in

  • G.P.

  • A.P.

  • Arithmetic − Geometric Progression

  • H.P.

Solution

D.

H.P.

WiredFaculty

Sponsor Area

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation