Principle Of Mathematical Induction
Sponsor Area
If A = 
and I = 
, then which one of the following holds for all n ≥ 1, by the principle of mathematical induction
-
An = nA – (n – 1)I
-
An = 2n-1A – (n – 1)I
-
An = nA + (n – 1)I
-
An = 2n-1A + (n – 1)I
A.
An = nA – (n – 1)I
By the principle of mathematical induction (1) is true.
Sponsor Area
If the number of terms in the expansion of 
is 28, then the sum of the coefficients of all the terms in this expansion is
-
64
-
2187
-
243
-
729
D.
729
Clearly, number of terms in the expansion of 
Let S(K) = 1 +3+5+..... (2K-1) = 3+K2. Then which of the following is true?
-
S(1) is correct
-
Principle of mathematical induction can be used to prove the formula
-
S(K) ≠S(K+1)
-
S(K)⇒ S(K+1)
D.
S(K)⇒ S(K+1)
S(K) = 1 + 3 + 5 + ...... + (2K - 1) = 3 + K2
Put K = 1 in both sides
∴ L.H.S = 1 and R.H.S. = 3 + 1 = 4 ⇒ L.H.S. ≠ R.H.S.
Put (K + 1) on both sides in the place of K L.H.S. = 1 + 3 + 5 + .... + (2K - 1) + (2K + 1)
R.H.S. = 3 + (K + 1)2 = 3 + K2 + 2K + 1
Let L.H.S. = R.H.S.
1 + 3 + 5 + ....... + (2K - 1) + (2K + 1) = 3 + K2 + 2K + 1
⇒ 1 + 3 + 5 + ........ + (2K - 1) = 3 + K2 If S(K) is true, then S(K + 1) is also true. Hence, S(K) ⇒ S(K + 1)
Maximum sum of coefficient in the expansion of (1 – x sinθ + x2 )n is
-
1
-
2n
-
3n
-
0
C.
3n
Sum of coefficients in (1 – x sinθ + x2 )n is (1 – sinθ + 1)n
(putting x = 1)
This sum is greatest when sinθ = –1, then maximum sum is 3n .
Statement − 1: For every natural number n ≥ 2 
Statement −2: For every natural number n ≥ 2,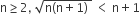
-
Statement −1 is false, Statement −2 is true
-
Statement −1 is true, Statement −2 is true, Statement −2 is a correct explanation for Statement −1
-
Statement −1 is true, Statement −2 is true; Statement −2 is not a correct explanation for Statement −1.
-
Statement − 1 is true, Statement − 2 is false.
C.
Statement −1 is true, Statement −2 is true; Statement −2 is not a correct explanation for Statement −1.
Hence Statement −2 is not a correct explanation of Statement −1.
Sponsor Area
Mock Test Series
Mock Test Series