A PHP Error was encountered
Severity: Notice
Message: Undefined variable: temp_qds
Filename: competition/Study_Question.php
Line Number: 141
Backtrace:
File: /home/wiredfa1/public_html/application/views/final/competition/Study_Question.php
Line: 141
Function: _error_handler
File: /home/wiredfa1/public_html/application/controllers/Competition.php
Line: 339
Function: view
File: /home/wiredfa1/public_html/index.php
Line: 315
Function: require_once
Application Of Integrals
Sponsor Area
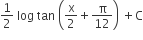
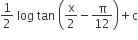
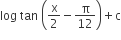
A.
Sponsor Area
-
e
-
e+1
-
e-1
-
1-e
e
e+1
1-e
C.
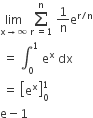
For x ∈, (0, 5π/2) define f(x). Then f (x) =  has
has
-
local maximum at π and 2π.
-
local minimum at π and 2π
-
local minimum at π and the local maximum at 2π.
-
local maximum at π and local minimum at 2π.
D.
local maximum at π and local minimum at 2π.
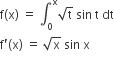
local maximum at π
and local minimum at 2π
If =-1 and x =2 are extreme points of f(x) =α log|x| + βx2 +x, then
-
α = -6, β = 1/2
-
α = -6, β = -1/2
-
α = 2, β = -1/2
-
α = 2, β = 1/2
C.
α = 2, β = -1/2
Here, x =-1 and x = 2 are extreme points of f(x) = α log|x| +βx2 +x then,
f'(x) = α/x +2βx + 1
f'(-1) = -α -2β +1 = 0 .... (i)
[At extreme point f'(x) = 0]
f'(2) = α/x +4βx + 1 = 0 .. (ii)
On solving Eqs (i) and (ii), we get
α = 2 and β = -1/2
If one of the diameters of the circle, given by the equation, x2+y2−4x+6y−12=0, is a chord of a circle S, whose centre is at (−3, 2), then the radius of S is:
-

-

-
5
-
10
B.

Given equation of a circle is x2 + y2 -4x +6y -12 = 0, whose centre is (2,-3) and radius
Now, according to given information, we have the following figure.
x2+y2-4x +6y-12 =0
Clearly, AO perpendicular to BC, as O is mid-point of the chord.
Now in ΔAOB,. we have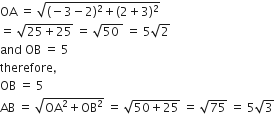
Sponsor Area
Mock Test Series
Mock Test Series