Application Of Derivatives
Sponsor Area
A spherical balloon is filled with 4500π cubic meters of helium gas. If a leak in the balloon causes the gas to escape at the rate of 72π cubic meters per minute, then the rate (in meters per minute) at which the radius of the balloon decreases 49 minutes after the leakage began is
-
9/7
-
7/9
-
2/9
-
9/2
C.
2/9
Volume of balloon is,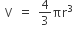
After 49 minutes volume = 4500π – 49 (72π) = 972π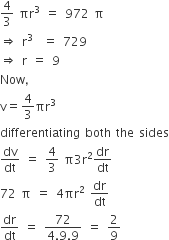
Sponsor Area
A wire of length 2 units is cut into two parts which are bent respectively to form a square of side=x units and a circle of radius=r units. If the sum of the areas of the square and the circle so formed is minimum, then:
-
2x=(π+4)r
-
(4−π)x=πr
-
x=2r
-
2x=r
C.
x=2r
According to give information, we have
Perimeter of a square + perimeter of a circle
= 2 units
⇒ 4 x + 2πr = 2
Now, let A be the sum of the areas of the square and the circle.
Then, A = x2 +π2r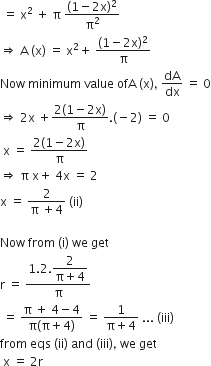
Equation of the ellipse whose axes are the axes of coordinates and which passes through the point (-3, 1) and has eccentricity  is
is
-
3x2 + 5y2 -32 = 0
-
5x2 + 3y2 - 48 = 0
-
3x2 + 5y2 - 15 = 0
-
5x2 + 3y2 - 32 = 0
A.
3x2 + 5y2 -32 = 0
B.
5x2 + 3y2 - 48 = 0
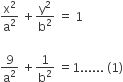
case - 1 when a > b
b2 = a2 (1 - e2)
b2 = a2 (1 - 2/5)
5b2 = 3a2......... (2)
from (1) & (2)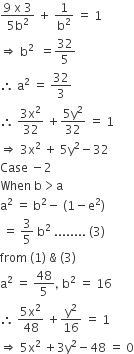
Given P(x) = x4+ ax3 + cx + d such that x = 0 is the only real root of P′ (x) = 0. If P(–1) < P(1),then in the interval [–1, 1].
-
P(–1) is the minimum and P(1) is the maximum of P
-
P(–1) is not minimum but P(1) is the maximum of P
-
P(–1) is the minimum but P(1) is not the maximum of P
-
neither P(–1) is the minimum nor P(1) is the maximum of P
B.
P(–1) is not minimum but P(1) is the maximum of P
P(x) = x4+ ax3+ bx2+ cx + d
P′(x) = 4x3+ 3ax2+ 2bx + c
As P′(x) = 0 has only root x = 0
⇒ c = 0
P′(x) = x(4x2+ 3ax + 2b)
⇒ 4x3+ 3ax + 2b = 0 has non real root.
and 4x2+ 3ax + 2b > 0 ∀ x ∈ [−1, 1].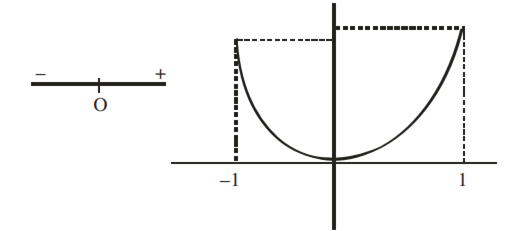
As P(−1) < P(1) ⇒ P(1) is the max. of P(x) in [−1, 1]
If 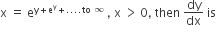
-
x /x+1
-
x-1/x
-
1/x
-
x+1/x
B.
x-1/x
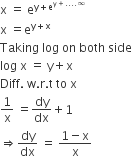
Sponsor Area
Mock Test Series
Mock Test Series





