Thermodynamics
Sponsor Area
(∆H −∆U) for the formation of carbon monoxide (CO) from its elements at 298 K is
(R = 8.314 J K–1 mol–1)
-
–1238.78 J mol–1
-
1238.78 J mol–1
-
–2477.57 J mol–1
-
2477.57 J mol–1
A.
–1238.78 J mol–1
∆H −∆U =∆ngRT
= (-1 x 8.314 x 298)/2
= - 1238.78
Sponsor Area
A piston filled with 0.04 mol of an ideal gas expands reversibly from 50.0 mL to 375 mL at a constant temperature of 37.00C. As it does so, it absorbs 208J of heat. The values of q and w for the process will be:(R = 8.314 J/mol K) ( ln 7.5 = 2.01)
-
q =+208J, W = - 208 J
-
q =-208 J, W =-208 J
-
q=-208J, W = +208 J
-
q =+208 J, W = +208 J
A.
q =+208J, W = - 208 J
From first law of thermodynamics, ΔE = q+W for an isothermal expansion.
Hence, q =-W
q= +208 J
W =-208 J [expansion work]
Consider the reaction: N2 +3H2 → 2NH3 carried out at constant temperature and pressure. If ∆H and ∆U are the enthalpy and internal energy changes for the reaction, which of the following expressions is true?
-
∆H = 0
-
∆H = ∆U
-
∆H < ∆U
-
∆H >∆U
C.
∆H < ∆U
∆H = ∆U + ∆nRT
∆n = -2
∆H = ∆U - 2RT
∆H < ∆U
For a particular reversible reaction at temperature T, ΔH and ΔS were found to be both +ve. If Te is the temperature at equilibrium, the reaction would be spontaneous when
-
Te>T
-
T >Te
-
Te is 5 times T
-
T=Te
A.
Te>T
For a particular reversible reaction at T temperature
ΔG = ΔH-TΔS
When ΔH, S is positive
ΔG = +ΔH- T (+ΔS)
For a spontaneous process, ΔG must be negative, it is possible only at high temperature.
That mean T> Te
For the complete combustion of ethanol, C2H5OH (l) + 3O2 (g) → 2CO2 (g) + 3H2O (l), the amount of heat produced as measured in a bomb calorimeter, is 1364.47 kJ mol-1 at 25oC. Assuming ideality the enthalpy of combustion, ∆CH, for the reaction will be (R = 8.314 JK-1 mol-1)
-
-1366.95 kJ mol-1
-
-1361.95 kJ mol-1
-
-1460.50 kJ mol-1
-
-1350.50 kJ mol-1
A.
-1366.95 kJ mol-1
C2H5OH (l) + 3O2 (g) → 2CO2 (g) + 3H2O (l),∆U = - 1364.47 kJ/mol
∆ng = -1
∆H = - 1364.47 +
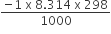
[Here, value of R in unit of J must be converted into kJ]
= - 1364.47-2.4776
= -1366.94 kJ/mol
Sponsor Area
Mock Test Series
Mock Test Series





