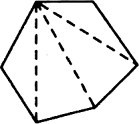
Examine the table. (Each figure is divided into triangles and the sum of the angles deduced from that).
Solution: From the above table, we conclude that sum of the interior angles of polygon with n-sides = (n - 2) x 180°
(a) When n = 7
Substituting n = 7 in the above formula, we have Sum of interior angles of a polygon of 7 sides (i.e. when n = 7)
= (n - 2) x 180° = (7 - 2) x 180°
= 5 x 180°
= 900°
(b) When n = 8
Substituting n = 8 in the above formula, we have
Sum of interior angles of a polygon having 8 sides
= (n - 2) x 180° = (8 - 2) x 180°
= 6 x 180°
= 1080°
(c) When n = 10
Substituting n = 10 in the above formula, we have
Sum of interior angles of a polygon having 10 sides
= (n - 2) x 180° = (10 - 2) x 180°
= 8 x 180°
= 1440°
(d) When n = n
The sum of interior angles of a polygon having n-sides = (n - 2) x 180°