Is 500 a perfect cube?
500 = 5 x 5 x 5 x 2 x 2
∵ In the above prime factorisation 2 x2 remain after grouping the prime factors in
triples.
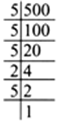
∴ 500 is not a perfect cube.
Sponsor Area
500 = 5 x 5 x 5 x 2 x 2
∵ In the above prime factorisation 2 x2 remain after grouping the prime factors in
triples.
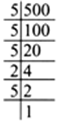
∴ 500 is not a perfect cube.
Sponsor Area
Is 1372 a perfect cube? If not, find the smallest natural number by which 1372 must be multipled so that the product is a perfect cube.
We have 1372 = 2 x 2 x 7 x 7 x 7
Since, the prime factor 2 does not appear in a group of triples. 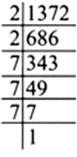
∴ 1372 is not a perfect cube.
Obviously, to make it a perfect cube we need one more 2 as its factor.
i.e. [1372] x 2 = [2 x 2 x 7 x 7 x 7] x 2
or 2744 = 2 x 2 x 2 x 7 x 7 x 7
which is a perfect cube.
Thus, the required smallest number = 2.
We hve 31944 = 2 x 2 x 2 x 3 x 11 x 11 x 11
Since, the prime factors of 31944 do not appear in triples as 3 is left over.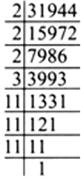
∴ 31944 is not a perfect cube, Obviously, 31944 ![]() will be a perfect cube
will be a perfect cube
i.e. [31944] ![]() 3 = [2 x 2 x 2 x 3 x 11 x 11 x 11]
3 = [2 x 2 x 2 x 3 x 11 x 11 x 11]![]() 3
3
or 10648 = 2 x 2 x 2 x 11 x 11 x 11
∴ 10648 is a perfect cube.
Thus, the required least number = 3.
Find the one’s digit of the cube of each of the following numbers.
(i) 3331 (ii) 8888 (iii) 149 (iv) 1005
(v) 1024 (vi) 77 (vii) 5022 (viii) 53
|
Number |
Number ending in |
Unit’s digit in the cube |
|
|
(i) |
3331 |
1 |
1 |
|
(ii) |
8888 |
8 |
2 |
|
(iii) |
149 |
9 |
9 |
|
(iv) |
1005 |
5 |
5 |
|
(v) |
1024 |
4 |
4 |
|
(vi) |
77 |
7 |
3 |
|
(vii) |
5022 |
2 |
8 |
|
(viii) |
53 |
3 |
7 |
Sponsor Area
Mock Test Series