Given, 
Charge, q₁= $5\times {10}^{-8 }\mathrm{C}$
Charge, q₂=–3 x 10^–8 C
Distance between the two charges, d= 16 cm

The possibility of point where total potential due to q₁ and q₂ is zero may be that point which lies out side the segment joining q₁ and q_2.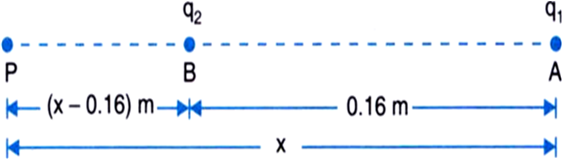


Let required point P lies 'x' distance away from ${\mathrm{q}}_1$ and (x-0.16) distance away from q₂ so that ${\mathrm{V}}_1+{\mathrm{V}}_2 = 0$.

where, V₁ is the potential at point P due to charge q₁ and,
V₂ is the potential at point P due to charge q_2. 
Now, using the forlmula for electrostatic potential at a given point we get, 
                     
$\therefore$                     $\frac{{\mathrm{Kq}}_1}{\mathrm{x}}+\frac{{\mathrm{Kq}}_2}{(\mathrm{x}-0.16)}=0$
           
             $\mathrm{K}\left[\frac{5\times {10}^{-8}}{\mathrm{x}}-\frac{3\times {10}^{-8}}{(\mathrm{x}-0.16)}\right] = 0$

$\Rightarrow$                         $\frac{5}{\mathrm{x}}-\frac{3}{\mathrm{x}-0.16} =0$
                         
$\Rightarrow$                         $\frac{5\mathrm{x}-0.8-3\mathrm{x}}{\mathrm{x}(\mathrm{x}-0.16)} = 0$

$\Rightarrow$                                 $2\mathrm{x}-0.8 = 0$

$$\begin{gathered} \Rightarrow \mathrm{x}=\frac{0.8}{2} \\ \Rightarrow \mathrm{x} = 0.4 \mathrm{m} \\ = 40 \mathrm{cm} \end{gathered}$$

That is, the required point is 40 cm away from  q₁ and (40 – 16) = 24 cm from q₂ such that, potential is 0.

Given,
$$\begin{gathered} C\mathrm{harge}, q = 5 \times {10}^{-6}\mathrm{C} \\ S\mathrm{ide} \mathrm{of} \mathrm{hexagon}, r = 10 \mathrm{cm} = 0.1 \mathrm{m} \end{gathered}$$ 

 

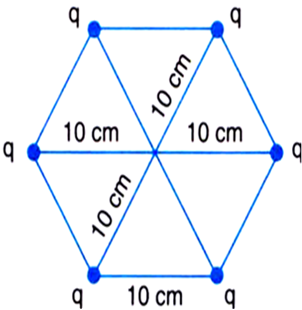
Potential at the centre of the hexagon is given by

Given two charges placed at points A and B.
 $$\begin{gathered} {\mathrm{q}}_1 = 2\mathrm{\mu C} = 2 \times {10}^{-6}\mathrm{C} \\ {\mathrm{q}}_2 = -2\mathrm{\mu c} = -2\times {10}^{-6}\mathrm{C} \\ \mathrm{r} =6 \mathrm{cm}= 0.06 \mathrm{m} \end{gathered}$$

(a) Potential will be zero due to both charges at equipotential surface

   $\frac{1}{4{\mathrm{\pi \epsilon }}_0}\left[\frac{{\mathrm{q}}_1}{\mathrm{x}}+\frac{{\mathrm{q}}_2}{(0.06-\mathrm{x})}\right] =0$

$\Rightarrow$                $\frac{{\mathrm{q}}_1}{\mathrm{x}} = -\frac{{\mathrm{q}}_2}{(0.06-\mathrm{x})}$

$\Rightarrow$         $\frac{2\times {10}^{-6}}{\mathrm{x}} = -\frac{\left(-2\times {10}^{-6}\right)}{\left[(0.06)-\mathrm{x}\right]}$

$\Rightarrow$                     $\mathrm{x} = 0.06 - \mathrm{x}$
$\Rightarrow$     $\mathrm{x}=\frac{0.06}{2} = 0.03 \mathrm{m}$

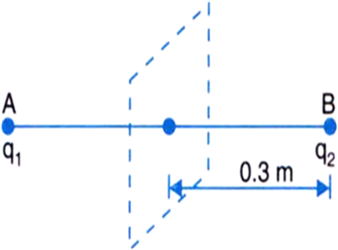
i.e., the plane normal to AB and passing through its mid-point has zero potential everywhere.

(b) The direction of electric field is normal to the plane in the AB direction.

Given,  
$\mathrm{Charge} \mathrm{on} \mathrm{conductor}, q = 1.6 \times {10}^{-7}\mathrm{C}$ 

$R\mathrm{adius} \mathrm{of} \mathrm{spherical} \mathrm{conductor}, r = 0.12 \mathrm{m}$

(a) Since, charge resides on the outer surface of the sphere, magnitude of electric field is 0 inside.

(b) Electric field just outside the sphere is given by
               
                      $$\begin{gathered} \boxed{\mathrm{E} = \frac{1}{4{\mathrm{\pi \epsilon }}_0}\frac{\mathrm{q}}{{\mathrm{r}}^2}} \\ = 9 \times {10}^9 \times \frac{1.6 \times {10}^{-7}}{(0.12{)}^2} \\ = {10}^5 {\mathrm{NC}}^{-1} \end{gathered}$$

(c) At a point 0.18 m from the centre of the sphere
                   $$\begin{gathered} \mathrm{E}= \frac{1}{4{\mathrm{\pi \epsilon }}_0}\frac{\mathrm{q}}{{\mathrm{r}}^2} \\ = 9 \times {10}^9 \times \frac{1.6 \times {10}^{-7}}{(0.18{)}^2} \\ = 4.4 \times {10}^4 {\mathrm{NC}}^{-1} \end{gathered}$$