+91-9350504919 support@wiredfaculty.com
Wired Faculty Logo
Wired Faculty Logo Wired Faculty

Sponsor Area

Some Applications of Trigonometry

Question
CBSEENMA10007606
Wired Faculty App

In ΔABC, right angled at B. AB = 24 cm, BC = 7 cm. Determine:
(i) sin A cos A,
(ii) sin C, cos C.

Solution

Let AB = 24 cm
BC = 7cm Using Pythagoras theorem, we have
AC2 = AB2 + BC2
= (24 cm)2+ (7 cm)2
= 576 cm2 + 49 cm2
= 625 cm2
So, AC = 25 cm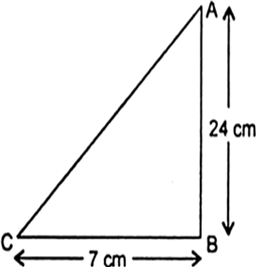
WiredFaculty
Now,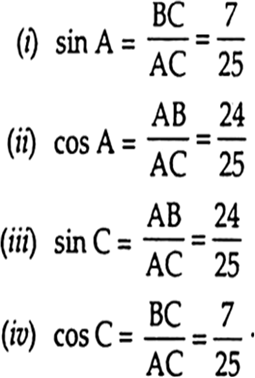
WiredFaculty

Question
CBSEENMA10007607
Wired Faculty App

In the given figure, find tan P - cot R.
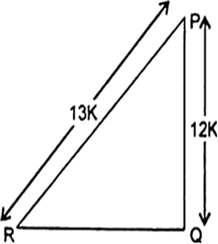
WiredFaculty

Solution

Let
PQ = 12K
and
PR = 13K
Using Pythagoras theorem, we have
PR2 = PQ2 + QR2
⇒(13K)2 = (12K)2 + QR2
⇒169K2 = 144K2 + QR2
⇒QR2 = 169K2 - 144K2
⇒QR2 = 25K2
So, QR = 5K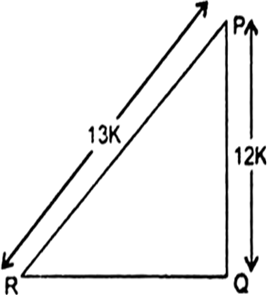
WiredFaculty
Now,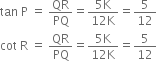 
WiredFaculty
Therefore,
tanP minus cotR space equals space 5 over 12 minus 5 over 12 equals 0.

Question
CBSEENMA10007608
Wired Faculty App

If sinA space equals space 3 over 4 comma space calculate cos A and tan A.

Solution

Let us draw a right angle triangle, right angled at B.
We know that:
space sin space straight A space equals space 3 over 4 space equals space BC over AC
 Let BC = 3K,  AC = 4K
where K is a positive number.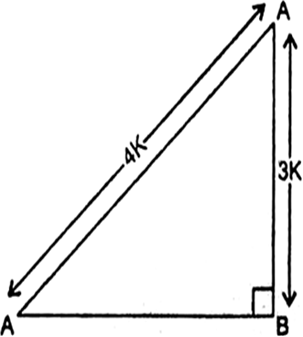
WiredFaculty
Using Pythagoras theorem, we have
                 WiredFaculty
rightwards double arrow        space space space space space space left parenthesis 4 straight K right parenthesis squared space equals space AB squared plus left parenthesis 3 straight K right parenthesis squared
rightwards double arrow              WiredFaculty
rightwards double arrow              space AB squared space equals space 16 straight K squared minus 9 straight K squared
rightwards double arrow               WiredFaculty
rightwards double arrow               WiredFaculty
Now,  cosA space equals space AB over AC equals fraction numerator square root of 7 straight K over denominator 4 straight K end fraction space equals fraction numerator square root of 7 over denominator 4 end fraction
and    tanA space equals space BC over AB equals fraction numerator 3 straight K over denominator square root of 7 straight K end fraction equals fraction numerator 3 over denominator square root of 7 end fraction.

Question
CBSEENMA10007609
Wired Faculty App

Given 15 cot A = 8, find sin A and sec A.

Solution

Let us draw a right triangle ABC, right angled at B.
It is given that:
15 cot A = 8
rightwards double arrow              space space cotA space equals space 8 over 15 equals AB over BC
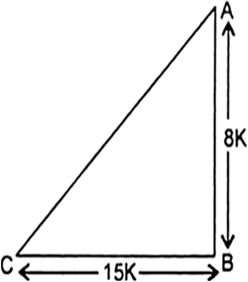
WiredFaculty

Let
AB = 8K, BC = 15K
Using Pythagoras theorem, we have
AC2 = AB2 + BC2 = (8K)2 + (15K)2
= 64K2 + 225K2
= 289K2
So,
AC = 17K
Now,
AC = 17K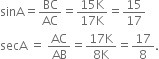
WiredFaculty

Sponsor Area

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation