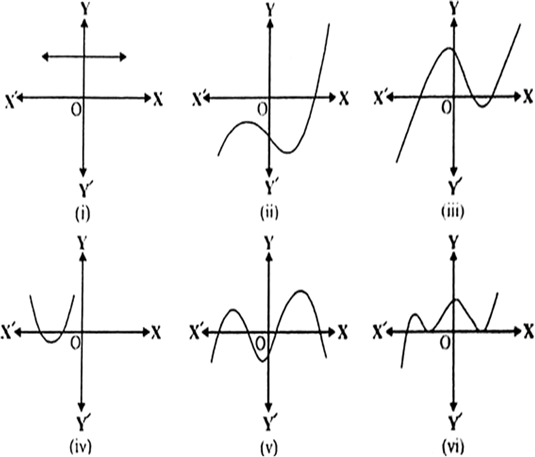
(i) Graph y = p(x) does not cut the x-axis at any point, so the given polynomial has no zero. (ii) Graph y = p(x) cuts the x-axis at one point, so the given polynomial has one zero. (iii) Graph y = p(x) cuts the x-axis at three points, so the given polynomial has three zeroes. (iv) Graph y = p(x) cuts the x-axis at two points, so the given polynomial has two zeroes. (v) Graph y = p(x) cuts the x-axis at four points, so the given polynomial has four zeroes. (vi) Graph y = p(x) cuts the x-axis at three points, so the given polynomial has three zeroes.

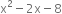
We have,
      
                              
So, the value of x² – 2x - 8 is zero when x - 4 = 0 or x + 2 = 0.
i.e., when x = 4 or x = –2.
Therefore, the zeroes of x² – 2x – 8 are 4 and - 2. Now,
   Sum of zeroes = (4) + (-2)
                           
Product of zeroes = (4) (-2)
                             

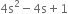
We have,
4s² – 4s + 1 = 4s² – 2s –2s + 1 = (2s–1)(2s– 1)
So, the value of 4s² – 4s + 1 is zero, when 2s – 1 = 0 or 2s – 1 = 0
i.e.  when   
Therefore, the zeroes of 4s² – 4s + 1 are  Now,
     Sum of zeroes =  
                             
Product of zeroes  = 
                              

We have,6x²–7x–3 = 6x²– 9x + 2x – 3
= 3x(2x – 3) + 1(2x – 3)
= (3x + 1) (2x – 3)
So, the value of 6x² – 7 – 3 is zero when (3a + 1) = 0 or (2x – 3) = 0
i.e.                 
Now, 
   Sum of zeroes  = 
                            
Product of zeroes = 
                            =