Sponsor Area
Arithmetic Progressions
In which of the following situations, does the list of numbers involved make an arithmetic progression, and why?
The taxi fare after each km when the fare is Rs. 15 for the first km and Rs. 8 for each additional km.
Taxi fare for 1 km = Rs. 15 = a1 Taxi fare for 2 kms
= Rs. 15 + Rs. 8 = Rs. 23 = a2 Taxi fare for 3 kms
= 23 + Rs. 8 = Rs. 31 = a3 Taxi fare for 4 kms
= Rs. 31 + Rs. 8 = Rs. 39 = a4
and so on.
a2 – a1 = Rs. 23 – Rs. 15 = Rs. 8
a3 – a2 = Rs. 31 – Rs. 23 = Rs. 8
a4 – a3 = Rs. 39 – Rs. 31 = Rs. 8
i.e., ak + 1 – ak is the same every time.
In which of the following situational, does the list of numbers involved make an arithmetic progression, and why?
The cost of digging a well for the first metre is Rs. 150 and rises by Rs. 50 for each succeeding metre.
Cost of digging the well after 1 metre of digging of Rs. 150 = a4
Cost of digging the well after 2 metres of digging
= Rs. 150 + Rs. 50
= Rs. 200 = a2
Cost of digging the well after 3 metres of digging
= Rs. 150 + Rs. 50
= Rs. 2a = a3
Cost of digging the well after 4 metres of digging
= Rs. 200 + Rs. 50
= Rs. 250 = a4
and so on.
a2 – a4 = Rs. 200 – Rs. 150 = Rs. 50
a3 – a2 = Rs. 250 – Rs. 200 = Rs. 50
a4 – a3 = Rs. 350 – Rs. 250 = Rs. 50
i.e., ak +1 – ak is the same every time.
So this list of numbers forms an A .P. with the first term a Rs. 150 and the common difference d = Rs. 50.
In which of the following situational, does the list of numbers involved make an arithmetic progression, and why?
The taxi fare after each km when the fare is Rs. 15 for the first km and Rs. 8 for each additional km.
Taxi fare for 1 km = Rs. 15 = a1 Taxi fare for 2 kms
= Rs. 15 + Rs. 8 = Rs. 23 = a2 Taxi fare for 3 kms
= 23 + Rs. 8 = Rs. 31 = a3 Taxi fare for 4 kms
= Rs. 31 + Rs. 8 = Rs. 39 = a4
and so on.
a2 – a1 = Rs. 23 – Rs. 15 = Rs. 8
a3 – a2 = Rs. 31 – Rs. 23 = Rs. 8
a4 – a3 = Rs. 39 – Rs. 31 = Rs. 8
i.e., ak + 1 – ak is the same every time.
So, this list of numbers form an arithmetic progression with the first term a = Rs. 15 and the common difference d = Rs. 8.
In which of the following situational, does the list of numbers involved make an arithmetic progression, and why?
The amount of air present in a cylinder when a vacuum pump removes  of the air remaining in the cylinder at a time.
of the air remaining in the cylinder at a time.
Amount of air present in the cylinder = x units (say) = a1
Amount of air present in the cylinder after one time removal of air by the vacuum pump![]()
Amount of air present in the cylinder after two times removal of air by the vacuum pump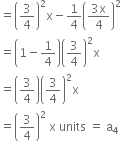
and so on,![]()
![]()
As a3 – a7 ≠ a3 – a2, this list of numbers does not form an A .P.
Sponsor Area
Mock Test Series
Mock Test Series





