Sponsor Area
Areas Related to Circles
Draw a line segment of length 7.6 cm and divide it in the ratio 5 : 8. Measure the two parts.
Steps of Construction :
(i) Draw AB = 5.6 cm
(ii) At a draw an acute ∠BAX below base AB.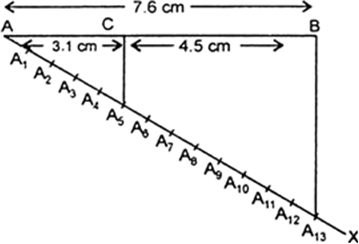
(iii) On AX make 5 + 8 i.e. 13 equal parts and mark them as A1, A2, A3, A4,... A13
(iv) Join B to A13. From A5 draw A5C || A13B. C is the required point of division and AC : CB = 5 : 8.
On measuring, we get
AC = 3.1 cm,
CB = 4.5 cm
Justification :
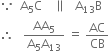
[Using basic proportionally theorem]
Therefore, 
This shows that C divides AB in the ratio 5 : 8.
Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides arc 
of the corresponding sides of the first triangle.
Steps of Construction :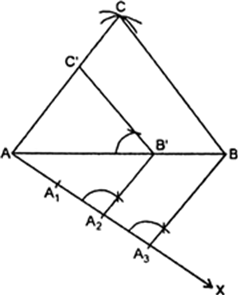
(i) Construct a ΔABC in which AB = 6 cm, AC = 4 cm, BC = 5 cm.
(ii) At A draw an acute ∠BAX below base AB.
(iii) Along AX mark off points A1, A2, A3 such that AA1 = A1 A1 = A2 A3.
(iv) Join A3B.
(v) From A2 draw A2B’ || A3B meeting AB at B’.
(vi) From B’ draw B‘C’ || CB meeting AC at C’. Thus, ΔAB‘C’ is the required triangle, each of whose sides is (2/3)rd of the corresponding sides of the ΔABC.
Justification :
[From (i)]
[By Basic proportionality theorem)
Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose sides arc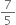 
of the corresponding sides of the first triangle.
Steps of Construction :
(i) Construct a ΔABC in which AB = 7cm, AC = 5 cm, BC = 6 cm.
(ii) At A draw an acute ΔBAX below base AB.
(iii) Along AX, mark off 7 points A1, A2, A1,.,
A7. Such that AA1 = A1 A2 = A2 A3
= A3 A4 =......= A6A7.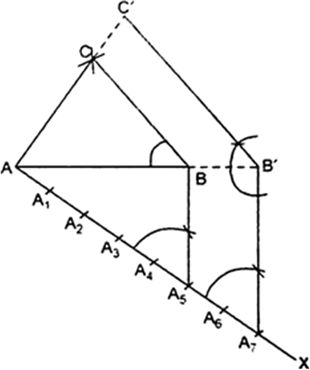
(iv) Join A5B.
(v) From A7 draw A7B’ || A5B meeting produced part of AB at B’.
(vi) From B’, draw B‘C’ || BC intersecting the extended line segment AC at C’.
Thus, AB‘C’ is the required triangle each of whose sides is 7/5 of the corresponding sides of the triangle ΔABC.
Justification :
Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another
triangle whose sides are 
times the corres ponding sides of the isosceles triangle.
Step of Construction :
(i) Draw a line segment BC = 8 cm.
(ii) Draw a perpendicular bisector AD (4 cm) of BC.
(iii) Joining AB and AC we get isosceles ΔABC.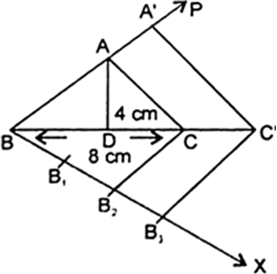
(iv) Construct an acute ∠CBX downwards.
(v) Along BX mark off 3 equal points B1, B2, B3 such that BB1 = B1B2 = B2B3.
(vi) Join C to B2 and draw a line through B3 parallel to B2C intersecting the extended line segment BC at C’.
(vii) Again draw a parallel line C’ A’ to AC cutting BP at A’.
(viii) ΔA ‘BC’ is the required triangle.
Justification :
C’A’ || CA [By construction] ΔABC ~ ΔA ‘BC’
[Using AA similarity condition]
Sponsor Area
Mock Test Series
Mock Test Series