Sponsor Area

Integrals

Question

Evaluate $integral from 1 to 2 of straight x space dx$ as the limit of a sum.

Solution

Comparing $integral from 1 to 2 of straight x space dx space space with space integral from straight a to straight b of straight f left parenthesis straight x right parenthesis space dx comma space space we space get comma$
$WiredFaculty$
$therefore space space space straight f left parenthesis straight a right parenthesis space equals space straight a comma space space straight f left parenthesis straight a plus straight h right parenthesis space equals space straight a plus straight h comma space space straight f left parenthesis straight a plus 2 straight h right parenthesis space equals space straight a plus 2 straight h comma space...... straight f left parenthesis straight a plus stack straight n minus 1 with bar on top straight h right parenthesis space equals space straight a plus left parenthesis straight n minus 1 right parenthesis straight h$
Now    $integral from straight a to straight b of straight f left parenthesis straight x right parenthesis space equals space stack Lt. straight h with straight h rightwards arrow 0 below left square bracket space straight f left parenthesis straight a right parenthesis plus straight f left parenthesis straight a plus straight h right parenthesis plus straight f left parenthesis straight a plus 2 straight h right parenthesis space plus space....... plus straight f left parenthesis straight a plus stack straight n minus 1 with bar on top space straight h right parenthesis right square bracket$
where n h = b - a
$rightwards double arrow$    $integral from straight a to straight b of xdx space equals space Lt with straight h rightwards arrow 0 below straight h left square bracket straight a plus straight a left parenthesis straight a plus straight h right parenthesis plus left parenthesis straight a plus 2 space straight h right parenthesis space plus space... plus left parenthesis straight a plus stack straight n minus 1 with bar on top straight h right parenthesis right square bracket$
   $equals stack Lt space straight h with straight h rightwards arrow 0 below left square bracket left parenthesis straight a plus straight a plus straight a plus... to space straight n space terms right parenthesis space plus space straight h open curly brackets 1 plus 2 plus 3 plus.... plus left parenthesis straight n minus 1 right parenthesis close curly brackets right square bracket$
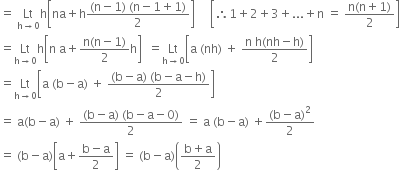
$WiredFaculty$
$therefore space space space space space integral from straight a to straight b of xdx space equals space 1 half left parenthesis straight b squared minus straight a squared right parenthesis$
Put a = 1, b = 2
$therefore space space space space space space space space space space space space space integral from 1 to 2 of xdx space equals space 1 half left parenthesis 4 minus 1 right parenthesis space equals space 3 over 2$

Question

Wired Faculty App

Evaluate the following definite integrals as limit of a sum.
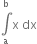
$integral from straight a to straight b of straight x space dx$

Solution

Comparing $integral subscript straight a superscript straight b xdx space space with space integral subscript straight a superscript straight b straight f left parenthesis straight x right parenthesis space dx comma space we space get$
$straight f left parenthesis straight x right parenthesis space equals space straight x$
$therefore$ $straight f left parenthesis straight a right parenthesis space equals space straight a plus straight h$
$straight f left parenthesis straight a plus 2 straight h right parenthesis space equals space straight a plus 2 straight h$
......................................
$straight f left parenthesis straight a plus stack straight n minus 1 with bar on top straight h right parenthesis space equals space straight a plus stack straight n minus 1 with bar on top straight h$
Now $integral subscript straight a superscript straight b straight f left parenthesis straight x right parenthesis space dx space equals space Lt with straight h rightwards arrow 0 below space straight h space left square bracket straight f left parenthesis straight a right parenthesis plus straight f left parenthesis straight a plus straight h right parenthesis plus straight f left parenthesis straight a plus 2 straight h right parenthesis plus.... plus straight f left parenthesis straight a plus stack straight n minus 1 with bar on top straight h right parenthesis right square bracket$
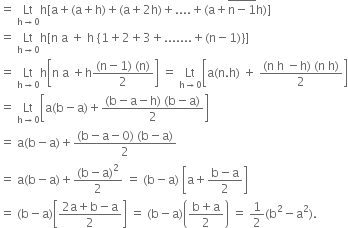
$WiredFaculty$

Question

Wired Faculty App

Evaluate the following definite integral as limit of a sum.
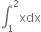
$integral subscript 1 superscript 2 xdx$

Solution

Comparing $integral subscript 1 superscript 2 xdx space with space integral subscript straight a superscript straight b straight f left parenthesis straight x right parenthesis space dx comma space space we space get comma$
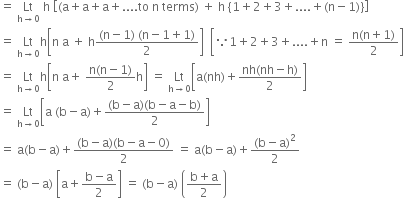
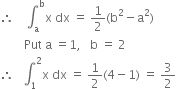
$WiredFaculty$
$therefore space space space space straight f left parenthesis straight a right parenthesis space equals space straight a comma space space straight f left parenthesis straight a plus straight h right parenthesis space equals space straight a plus straight h comma space space straight f left parenthesis straight a plus 2 straight h right parenthesis space equals space straight a plus 2 straight h comma space...... comma space straight f left parenthesis straight a plus stack straight n minus 1 with bar on top straight h right parenthesis space equals space straight a plus left parenthesis straight n minus 1 right parenthesis space straight h$
Now $integral subscript straight a superscript straight b straight f left parenthesis straight x right parenthesis space equals space Lt with straight h rightwards arrow 0 below space straight h open square brackets straight f left parenthesis straight a right parenthesis plus straight f left parenthesis straight a plus straight h right parenthesis plus straight f left parenthesis straight a plus 2 straight h right parenthesis plus... plus straight f left parenthesis straight a plus stack straight n minus 1 with bar on top straight h right parenthesis close square brackets$
$rightwards double arrow$ $integral subscript straight a superscript straight b xdx space equals space Lt with straight h rightwards arrow 0 below straight h space left square bracket straight a plus left parenthesis straight a plus straight h right parenthesis plus left parenthesis straight a plus 2 straight h right parenthesis plus... plus left parenthesis straight a plus stack straight n minus 1 with bar on top space straight h right parenthesis right square bracket$
$WiredFaculty$
$WiredFaculty$

Question

Wired Faculty App

Evaluate the following definite integral as limit of a sum.
$integral subscript 0 superscript 5 left parenthesis straight x minus 1 right parenthesis dx$

Solution

Comparing $integral subscript 0 superscript 5 left parenthesis straight x minus 1 right parenthesis dx space with space integral subscript straight a superscript straight b space straight f left parenthesis straight x right parenthesis space dx comma space space space we space get comma$
f(x) = x - 1, a = 0, b = 5
$straight f left parenthesis straight a plus 2 space straight h right parenthesis space equals space straight f left parenthesis 2 space straight h right parenthesis space equals space 2 space straight h space minus space 1 comma space space..... comma space space left parenthesis straight a plus stack straight n minus 1 with bar on top straight h right parenthesis space equals space straight f left parenthesis stack straight n minus 1 with bar on top straight h right parenthesis space equals space left parenthesis straight n minus 1 right parenthesis space straight h space minus 1$
Now $integral subscript straight a superscript straight b straight f left parenthesis straight x right parenthesis space equals space Lt with straight h rightwards arrow 0 below space straight h open square brackets straight f left parenthesis straight a right parenthesis plus straight f left parenthesis straight a plus straight h right parenthesis plus straight f left parenthesis straight a plus 2 straight h right parenthesis plus... plus straight f left parenthesis straight a plus stack straight n minus 1 with bar on top straight h right parenthesis close square brackets$
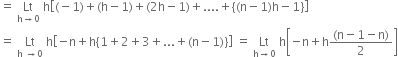
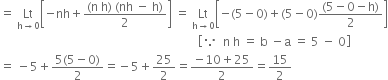
$WiredFaculty$ $WiredFaculty$
$WiredFaculty$

Sponsor Area

For Daily Free Study Material Join wiredfaculty

WhatsApp Group

Download Android App

Ncert Book Download

Integrals

Evaluate $integral from 1 to 2 of straight x space dx$ as the limit of a sum.

Evaluate the following definite integrals as limit of a sum.
$integral from straight a to straight b of straight x space dx$

Evaluate the following definite integral as limit of a sum.
$integral subscript 1 superscript 2 xdx$

Evaluate the following definite integral as limit of a sum.
$integral subscript 0 superscript 5 left parenthesis straight x minus 1 right parenthesis dx$

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

For Daily Free Study Material Join wiredfaculty

WhatsApp Group

Download Android App

Ncert Book Download

Integrals

Evaluate as the limit of a sum.

Evaluate the following definite integrals as limit of a sum.

Evaluate the following definite integral as limit of a sum.

Evaluate the following definite integral as limit of a sum.

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Evaluate $integral from 1 to 2 of straight x space dx$ as the limit of a sum.

Evaluate the following definite integrals as limit of a sum.
$integral from straight a to straight b of straight x space dx$

Evaluate the following definite integral as limit of a sum.
$integral subscript 1 superscript 2 xdx$

Evaluate the following definite integral as limit of a sum.
$integral subscript 0 superscript 5 left parenthesis straight x minus 1 right parenthesis dx$