Let y = f(x) be equation of curve.
Now  is the slope of the tangent to the curve at the point (x, y)
From the given condition, 
          
Separating the variables,  we get,
                           
Integrating, 
                                  ...(1)
Since curve passe through (-2, 1)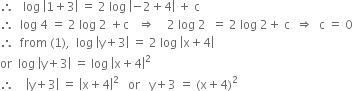

which is required equation of curve.

The given differential equation is
                        sin x cos y dx + cos x sin y dy = 0
  or          sin x cos y dx =  - cos x sin y dy

Integrating 

Since the curve passes through 

The given differential equation is
            y' = e^x sin x  or   
Separating the variables,  we get,
                       
Integrating,  

                                 
                         ...(1)
Now curve passes through (0, 0)

Let v be volume of spherical balloon of radius r.
                                   ...(1)
From given condition,
                               

Separating the variables and integrating, we get.
              ...(2)
Now t = 0 when r = 3
                ...(3)
Again   t = 3  when r = 6
                                    


Putting