Sponsor Area
Current Electricity
The storage battery of a car has an emf of 12 V. If the internal resistance of the battery is 0.4 Ω , what is the maximum current that can be drawn from the battery?
Maximum current is drawn from a battery when the external resistance in the circuit is zero i.e., R = 0.
Given,
E.m.f of the battery,
Internal resistamce of the battery,
Therefore, using the formula for maximum current drawn we get,
A battery of emf 10 V and internal resistance 3 Ω is connected to a resistor. If the current in the circuit is 0.5 A, what is the resistance of the resistor? What is the terminal voltage of the battery when the circuit is closed?
Given,
EMF of battery,
Internal resistance of battery, r=
Current flowing in the circuit, I= 0.5 A
Using the forlmula
or
where, R is the external resistance.
is the required resistance.
Terminal voltage,
a) Three resistors 1 Ω, 2Ω, and 3 Ω are combined in series. What is the total resistance of the combination?
b) If the combination is connected to a battery of EMF 12 V and negligible internal resistance, obtain the potential drop across each resistor.
Given, three resistors of resistances 1 combined in series.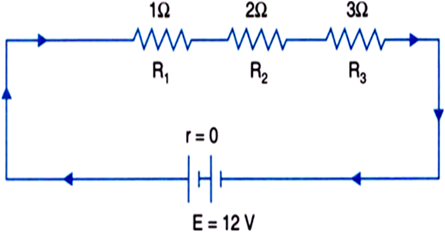
a) Total resistance of series combination is given by,
b) If the combination is connected to a battery of 12 V and negligible internal resistance.
Current through the circuit,
Potential drop across R1 = 2 x 1 V = 2 V
Potential drop across R2 = 2 x 2 V = 4 V
Potential drop across R3 = 2 x 3 V = 6V
i) Three resistors 2 Ω, 4 Ω and 5 Ω are combined in parallel. What is the total resistance of the combination?
ii) If the combination is connected to a battery of emf 20 V and negligible internal resistance, determine the current through each resistor, and the total current drawn from the battery.
Given, three resistors 2 are combined in parallel. 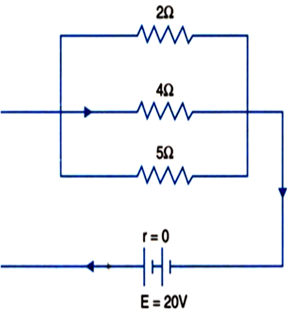
Therefore,
Total resistance of parallel combination,
ii) The combination is connected to a battery of 20 V.
Let the current through resistances 2Ω, 4Ω and 5Ω are I1, I2 and I3 respectively.
Now, using Ohm's law across each resistor we get,
Hence,
Total current is given by
Sponsor Area
Mock Test Series
Mock Test Series





