Sponsor Area
Wave Particle Duality: Matter Waves
Question
What is the relation between wavelength and momentum of moving particles?
Solution
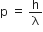 ;
;
where,
p = momentum
h = planck's constant  = wavelength
= wavelength
Question
Calculate the energy released when an electron annihilates a positron.
Solution
Energy of equivalent of mass of electron and positron.
Eo = moC2
= (9.1 x 10-31 X3 x 108 )2
= 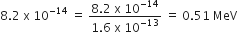
Energy released = 0.51 x 2 = 1.02 MeV
Question
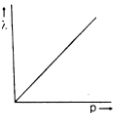
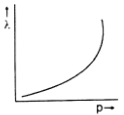
Which one of the following graphs in Figure 1 represents variation of de Broglie wavelength (λ) of particle having linear momentum p:
-
-
-
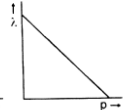
-
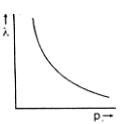




Solution
D.

Question
De Broglie wavelength of electrons of kinetic energy E is λ. What will be its value if kinetic energy of electrons is made 4E?
Solution
De Broglie’s wavelength of electron = λ
Let the new wavelength be λ2
K.E. of electrons = E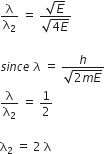
Sponsor Area
Mock Test Series
Mock Test Series





