Sponsor Area
Refraction Of Light At Spherical Surfaces: Lenses
Find the focal length and nature of a lens whose optical power is - 5D.
Focal length, f = -1/5 = 0.02 m.
Nature of the lens = Concave lens
A convex lens ‘L’ and a plane mirror ‘M’ are arranged as shown in Figure 8 below. Position of object pin ‘O’ is adjusted in such a way that the inverted image ‘I’ formed by the lens mirror combination, coincides with the object pin ‘s. Explain how and when this happens.
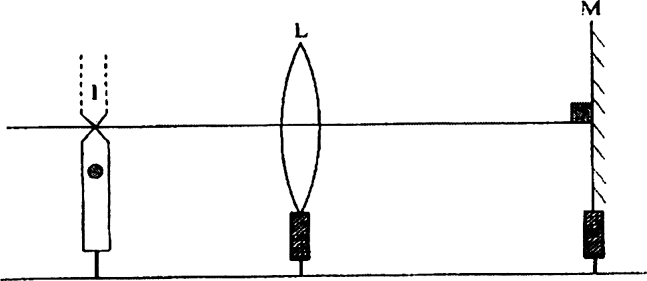
If object pin is rept exactly at the focus of convex lens rays emerging out of the lens towards the mirror will be parallel. These rays which are perpendicular to surface of plane mirror are reflected along same path, got reflected and form image at F.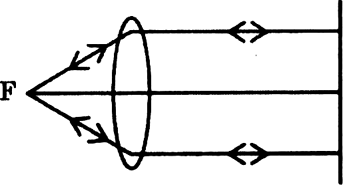
Starting with an expression for refraction at a single spherical surface obtain an expression for lens maker’s formula.
Lens makers formula: It relates focal length of a lens of the refractive index of material of lens and radii of curvature of two surfaces of lens.
Let us consider a conves lens of glass having RI n2 placed in rarer medium of Rln1. P1 and P2 be poles of C1 and C2. R1= (P1C1), R2 = (P2C2). τ= P1P2(thickness of lens).
Let a point object O be placed on principal axis at a distance is u from P1. A ray OA travelling in rarer medium is incident on first surface of lens. It is refracted towards normal at A.
If the second surface of lens were absent, the ray AB would have met the principle axis at I’ which is image of V.
Let the distance of I1 from P1 be V1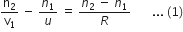
The roy AB travelling in medium n2 is actually incident an second surface of lens and refracted into rarer medium n1 bending away from normal at B. The emergent ray meets principal axis at I which is final real image of O.
For refraction at second surface I acts as vertual image and I is real image, v → distance of I from P2. 
Show that the axial chromatic aberration (fr-fv) for a convex lens is equal to the product of its mean focal length (f) and dispersive power (ω ) of its material i.e. Prove : (fr-fv ) = ω f.
Let the mean refractive index of the material of the lens be n1 and the mean focal length of the lens be fy.
From lens makes formule, 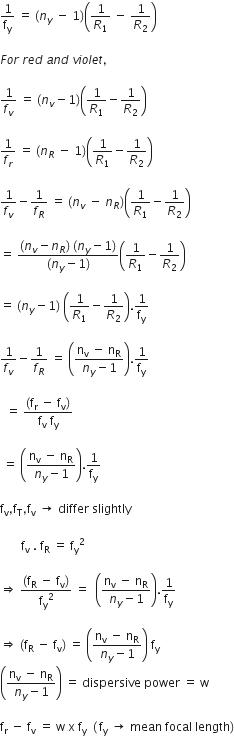
Sponsor Area
Mock Test Series
Mock Test Series





