Sponsor Area
Magnetic Torque On A Current Loop: Moving Coil Galvanometer
In a moving coil galvanometer, what is meant by a radial magnetic field?
When the magnet are grounded concave, the fields lines then pass radially by across the pole pieces such a field is known as radial field.
Using either deflection magnetometer or vibration magnetometer, explain how will you compare magnetic moments of two given bar magnets.
Using Deflection Galvanometer:
We can use deflection galvanometer by setting it in end-on position or broad side-on position,
(i) By setting the magnetometer in end-on position : When the deflection magnetometer is placed so that the two arms of the magnetometer and 0°-0° line lie along east-west line, the magnetometer is said to be placed in end-on position.
So the horizontal component of earth’s magnetic field (BH) is perpendicular to the magnetic field (B) produced by the bar magnet as shown in figure.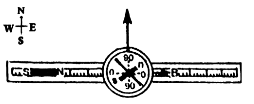
Magnetic moment can be compared by using deflection method or null method.
Consider two equal bar magnets A and B having magnetic moments M1 and M2 respectively.
Let l be length of the each magnet. Place magnet A on the arm of the magnetometer lengthwise r at a distance effect of an r from the centre of the magnetometer.
Let B1 be magnetic field due to magnet at the centre of the magnetometer box.
If the magnetic needle ns of the magnetometer box deflect at an angle θ, then,
B1 = BH tanθ1 ...(1)
Since, magnetic needle lies on the axial line of the magnet,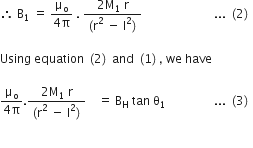
Place magnet B in place of magnet A at the same distance r from the centre of the magnetometer, magnetic needle deflects at an angle 02, then as obtained in case of magnet A, we have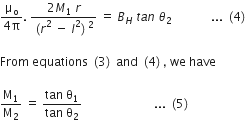
By calculating θ1 and θ2 the ratio Ml/M2 can be calculated.
ii)
By setting the magnetometer in broad side-on position :
When the deflection magnetometer is placed, so that the arms of the magnetomer and 90°-90° line lie along the N-S magnetometer is said to be placed in broad side-on position.
The horizontal component of earth’s magnetic field to magnetic’s magnetic field.
Let M1and M2 magnetic moments of magnets A and B.
2l be length of each magnet.
Place magnet A on the arm of magnetometer breadthwise at a distance r from the centre of the box as shown in figure. 
Let B1 be the magnetic field due to the centre of the magnetometer box. If the magnetic needle ns deflects through angle θ1, then
B = BHtan θ1 ...(6)
magnetic needle lies on the equitorial line of the magnet.
B1 = 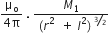
Using B1 in equation, we have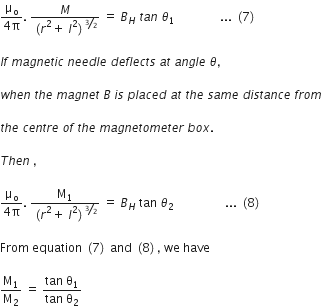
Calculate the magnetic field (in SI unit) at the centre of a tangent galvanometer coil of 50 turns and radius 10 cm when a current of 1.0 A passes through it.
Magnetic field at the centre of the tangent galvanometer is given by,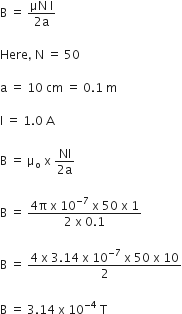
Obtain the formula, I = k θ for a moving coil galvanometer, given, the deflecting torque 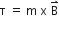 where m is the magnetic dipole moment of the coil placed in the magnetic field B, I is the current in the galvanometer and θ is the deflection.
where m is the magnetic dipole moment of the coil placed in the magnetic field B, I is the current in the galvanometer and θ is the deflection.
Suppose the rectangular coil ABCD having n turns is of length and breadth b is placed in magnetic field B.
When current is passed through the coil, forces act on all the arms of the coil. DA and BC being equal and opposite, cancel the effect of each other. If current is passed in the direction of ABCD, then force on arm AB,
F = n B Il (normally outwards)
and
Force on arm CD, F = n B Il (normally inwards)
The two forces are equal, opposite, parallel and act at different points as shown in above figure.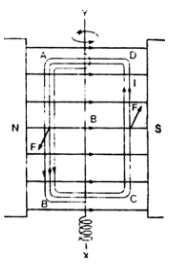
Hence, the two forces constitute a torque.
As the coil rotates under the effect of the torque, the suspension wire gets twisted and restoring torque is developed in the suspension wire.
The coil will rotate, till the deflecting torque acting on the coil due to flow of current is balanced by the restoring torque developed in the suspension wire due to twisting.
Therefore, in equilibrium,
Deflecting torque = restoring torque (in magnitude)
Suppose the coil comes to rest after rotating through an angle 0. In this position, the plane of the coil makes angle θ. with the direction of the field as shown in Fig. 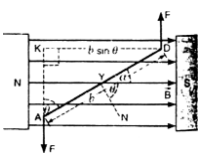
The perpendicular distance between the forces acting on arms AB and CE is given by
DK = AD cos θ = b cos θ.
Therefore, deflecting torque acting on coil = either force x DK = n B I l x b cosθ= n BI A cosθ.
Where A = l x b is the area of the coil. If k is the restoring torque per unit twist for the material of the suspension wire, then restoring torque = kθ.
Since in equilibrium, the restoring torque is just equal and opposite the the deflecting torque,
n B I A cos θ= kθ
I = 
Since the factor,  , is constant for the given galvanometer.
, is constant for the given galvanometer.
I 
As the deflection (θ) produced is not directly proportional to the current (I) passing through the galvanometer, a linear scale cannot be used for measuring the current.
In order that deflection produced in the coil of the galvanometer may be directly proportional to the current passed, the poles of the magnet are made concave so as to produce radial magnetic field.
In such a field, the plane of the coil is parallel to the magnetic lines of force in all positions of the coil figure and hence perpendicular distance between the forces on the two arms of the coil is always equal to 6, the breadth of the coil. 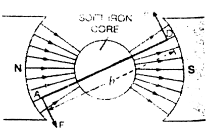
Therefore, in case of radial magnetic field,
Deflecting torque = nBIl x v = n BIA
In equilibrium,
nBIA = k
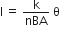
I = Gθ
where, 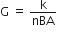 , is constant for a galvanometer and is called galvanometer constant.
, is constant for a galvanometer and is called galvanometer constant.
Hence, I ∝ θ
I = k 
Sponsor Area
Mock Test Series
Mock Test Series





