Sponsor Area
Magnetic Effect Of Current
The Biot Savart’s Law in vector form is:
-
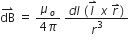
-
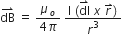
-
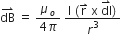
-
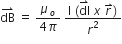
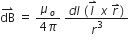
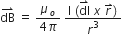
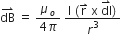
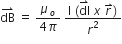
B.
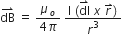
State the SI unit of magnetic dipole moment.
Ampre-metre2
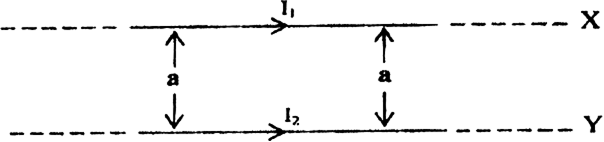
Figure below shows two infinitely long and thin current carrying conductors X and Y kept in vacuum, parallel to each other, at a distance ‘a’.
(i) How much force per unit length acts on the conductor Y due to the current flowing througn X? Write your answer in terms of 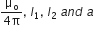 .
. 
(ii) Define ampere, in terms of froce between two current carrying conductors.
i) Force applied per unit length is given by,
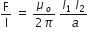
ii) One ampere is the current which when flowing in each of two infinitely long parallel conductors 1 m apart in vaccum produces between them a force of exactly 2 x 10-10 Newton per metre of length.
When a charged particle is projected perpendicular to a uniform magnetic field, it describes a circular path in which:
-
its speed remains constant
-
its velocity remains constant.
-
its velocity remains constant.
-
its kinetic energy increases.
A.
its speed remains constantSponsor Area
Mock Test Series
Mock Test Series





