Sponsor Area
DC Circuits And Measurements
In the circuit shown in Figure 3, E1 = 17V,E2 = 21V, R1 = 2μ, R2=3μ R1=2μ R2= 3μ and R3 = 5μ.
Using Kirchoffs laws, find the currents flowing through the resistors R1,R2 and R3. (Internal resistance of each of the batteries is neglegible.)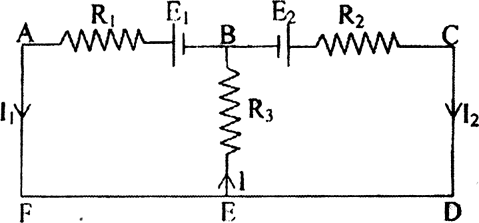
(a) Applying Kirchoffs voltage Law to Loop ABEF
R1l1 + IR3 - E1 = 0 2I1 + 5I
= 17 I = I1 + l2 2I1 + 5I1 + 5l1
= 17
7I1 + 5I2 = 17 ... (i)
Applying voltage law to Loop BCDE, we have
R2I2 + R3I - 2I = 0 3I2 + 5I1 + 5I2
= 21
5I1 + 8I2 = 21 ... (ii)
Solving equations (i) and (ii)
Multiplying eq. (1) by 5 throughout
[ 7I1 + 5I2 = 17] x5
35I1 + 25I2 = 85 ... (iii)
Multiplying eq. (2) by 7 throughout, we get
[ 5I1 + 8I2 = 21 ] x7
35I1 + 56I2 = 147 ... (iv)
On solving equations (iii) and (iv), we get
-31 I2 = -62
This implies,
I2 = 2 Amp, and
I1 = 1 Amp
Current in R1=I1 = 1 Amp
Current in R2 =I2 = 2 Amp
Therefore,
Current in R3 =I1+I2 = 3 Amp
Which conservation principle is involved in Kirchoffs first law of electric circuits?
Law of Conservation of charge.
In the circuit shown in Figure 4 below, E is a battery of emf 6V and internal resistance 1Ω. Find the reading of the ammeter A, if it has negligible resistance :
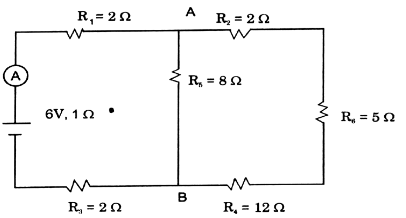
Equivalent resistors across the terminal AB is given by, 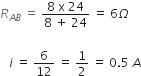
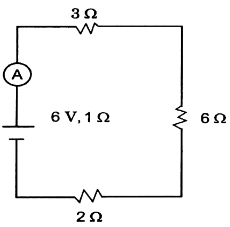
Reading on the ammeter = 0.5 A
With the help of a neatly drawn and lebelled diagram, obtain balancing condition of a Wheatstone bridge.
Current are distributed as shown in the figure below.
Resistances P, Q, R and S are shown.
Division of current are marked.
Applying KVL to the mesh ABD,
i1P + igG - (i - i1)R = 0 ---(i)
Applying KVL to the mash BCD,
(ii - ig)Q - (i - ii + ig)s - igG =0 ---(ii)
under balanced condition ig = 0
ii P = (i - ii)R ---(iii)
ii Q = (i - ii)S ---(iv)
Dividing eq. (iii) by eq. (iv)
Sponsor Area
Mock Test Series
Mock Test Series





