Sponsor Area
रेखाएँ और कोण
आकृति में, रेखाएँ AB और CD बिंदु O पर प्रतिच्छेदित करती हैं। यदि ∠AOC + ∠BOE = 70° है और ∠BOD = 40° है, तो ∠BOE और प्रतिवर्ती ∠COE ज्ञात कीजिए।
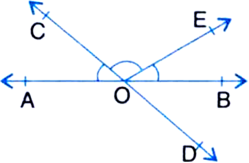
∠AOC + ∠BOE = 70o
∠BOD = 40o ...(i)
∴ ∠AOC = ∠BOD [ शीर्षाभिमुख कोण ]
∴ ∠AOC = 40° ...(ii)
अब, ∠AOC + ∠BOE = 70°
⇒ 40° + ∠BOE = 70°
⇒ ∠BOE = 70° - 40°
⇒ ∠BOE = 30°
= ∠COD + ∠BOD + ∠BOE
= ∠COD + 40° + 30°
समीकरण (i) और (ii) से
∠COE + 40° + 30° = 180o ⇒ ∠COE = 110o
प्रतिवर्ती
∠COE = 360o - 110o =- 250o
आकृति में, रेखाएँ XY और MN बिंदु O पर प्रतिच्छेद करती हैं। यदि 
= 90° और a : b = 2 : 3 हैं, तो c ज्ञात कीजिए।
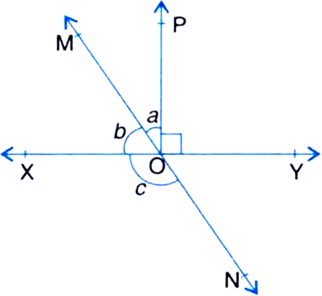
[ एक ही रेखा पर बने कोण ]
a + b = 900 .....(1)a : 2 = 2 : 3
a = 2kb = 3k
दोनों का मान समीकरण (i) में रखने पर
2k + 3k = 900
= 180° [ एक ही रेखा पर बने कोण ]⇒ b + c = 180°
⇒ 54° + c = 180°
⇒ c = 180° - 54°
⇒ c = 126°
आकृति में, यदि ∠PQR = ∠PRQ है, तो सिद्ध कीजिए कि : ∠PQS = ∠PRT
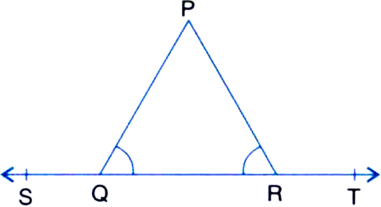
आकृति में, 
∴ ∠PQS + ∠PQR = 180° ...(1)
[ रैखिक कोण ]
∴ ∠PRQ + ∠PRT = 180° ...(2)
[ रैखिक कोण ]
समीकरण (i) और (ii) से
∠PQS + ∠PQR = ∠PRQ + ∠PRT
⇒ 
⇒ ∠PQS = ∠PRT
आकृति में, यदि x + y = w + z है, तो सिद्ध कीजिए कि AOB एक रेखा है।
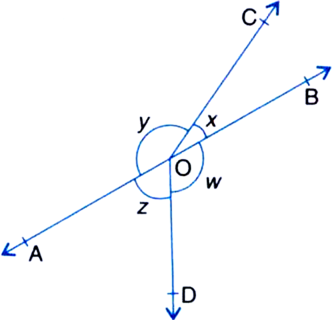
x + y = w + z ...(i) [ दिया है ]
∵ एक बिंदु के चरों ओर बने कोण = 360°
x + y + w + z = 360o
x + y + x + y = 360o
2(x + y) = 360o
x + y = 180
∴ AOB एक सरल रेखा है।
Sponsor Area
Mock Test Series
Mock Test Series