Sponsor Area
त्रिभुज
चतुर्भुज ACBD में, AC = AD है और AB कोण A समद्विभाजित करता है। दर्शाइए कि ∆ABC ≅ ∆ABD है। BC और BD के बारे में आप क्या कह सकते हैं?
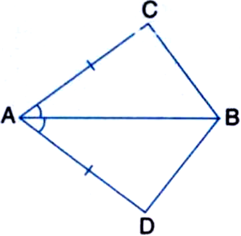
दिया है: चतुर्भुज ACBD में, AC = AD और AB कोण A का समद्विभाजक है
सिद्ध करना है: ∆ABC ≅ ∆ABD
∆ABC और ∆ABD में
AC = AD
AB = AB [ उभयनिष्ठ ]
∠CAB = ∠DAB
[ ∵ AB कोण A का समद्विभाजक है ]
∴ ∠ABC ≅ ∠ABD ( SAS सर्वांगसमता )
∴ BC = BD
ABCD एक चतुर्भुज है, AD = BC और ∠DAB = ∠CBA है। सिद्ध कीजिए कि:
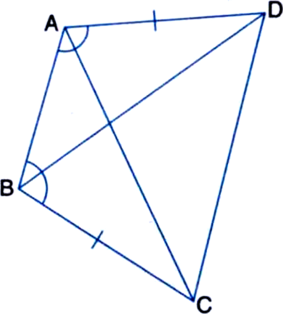
(i) ∆ABD ≅ ∆BAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC
दिया है: ABCD एक चतुर्भुज है, AD = BC और ∠DAB = ∠CBA
सिद्ध करना है: (i) ∆ABD ≅ ∆BAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC.
(i) ∆ABD और ∆BAC में,
AD = BC
AB = BA [ उभयनिष्ठ ]
∠DAB = ∠CBA
∴ ∆ABD ≅ ∠BAC [ SAS सर्वांगसमता ]
(ii) ∵ ∆ABD ≅ ∆BAC
∴ BD = AC
(iii) ∵ ∆ABD ≅ ∠BAC
∴ ∠ABD = ∠BAC
एक रेखाखंड AB पर AD और BC दो बराबर लंब रेखाखंड हैं। दर्शाइए कि CD रेखाखंड AB को समद्विभाजित करता है।
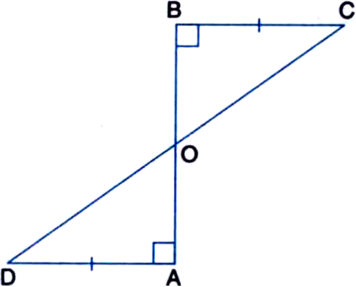
दिया है: AD और BC रेखाखंड AB पर लंब हैं।
सिद्ध करना है: CD रेखाखंड AB को समद्विभाजित करता है OA =OB
∆OAD और ∆OBC में,
AD = BC
∠OAD = ∠OBC [ प्रत्येक कोण = 90° ]
∠AOD = ∠BOC [ समुख कोण ]
∴ ∠OAD ≅ ∆OBC [ ASA सर्वांगसमता ]
∴ OA = OB
∴ CD रेखाखंड AB को समद्विभाजित करता है OA =OB
l और m दो समांतर रेखाएँ हैं जिन्हें समांतर रेखाओं p और q का एक अन्य युग्म प्रतिच्छेदित करता है। दर्शाइए कि ∆ABC ≅ ∆CDA
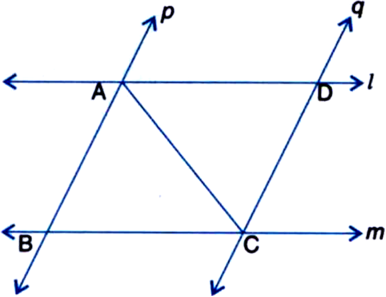
∵ AB || DC
और AD || BC
∴ चतुर्भुज ABCD एक समांतर चतुर्भुज है
∵ एक चतुर्भुज एक समांतर चतुर्भुज होगी यदि दोनों विपरीत भुजाएं समांतर हों
∴ BC = AD ... (i)
AB = CD ... (ii)
और ∠ABC = ∠CDA ... (iii)
∆ABC और ∆CDA में,
AB = CD
BC = DA
∠ABC = ∠CDA [ समीकरण (iii) से ]
∴ ∆ABC ≅ ∆CDA [ ASA सर्वांगसमता ]
Sponsor Area
Mock Test Series
Mock Test Series





