Sponsor Area
प्रायोगिक ज्यामिति
अरशद के पास एक चतुर्भुज ABCD की पाँच माप हैं। ये माप AB = 5 cm, ![]() , AC = 4 cm, BD = 5 cm और AD = 6 cm हैं। क्या वह इन मापों से एक अद्वितीय चतुर्भुज बना सकता है? अपने उत्तर के कारण दीजिए।
, AC = 4 cm, BD = 5 cm और AD = 6 cm हैं। क्या वह इन मापों से एक अद्वितीय चतुर्भुज बना सकता है? अपने उत्तर के कारण दीजिए।
दिए गए आँकड़ों से वह चतुर्भुज ABCD नहीं बना सकता जिसके निम्न कारण हैं:
यदि हम पहले विकर्ण BD लेते हैं तो पहला ![]() बना लेते हैं परन्तु दूसरा
बना लेते हैं परन्तु दूसरा ![]() नहीं बना सकते क्योंकि इसकी केवल एक भुजा दी गई हैं।
नहीं बना सकते क्योंकि इसकी केवल एक भुजा दी गई हैं।
यदि हम केवल विकर्ण AC लेते हैं तो ![]() और
और ![]() को बनाने के लिए पर्याप्त आँकड़े नहीं हैं।
को बनाने के लिए पर्याप्त आँकड़े नहीं हैं।
हमने देखा कि एक चतुर्भुज की पाँच मापों से एक अद्वितीय चतुर्भुज की रचना की जा सकती है। क्या आप सोचते हैं कि चतुर्भुज की किन्हीं पाँच मापों से ऐसी रचना की जा सकती है?
एक चतुर्भुज के बनाने के लिए 5 भागों का होना आवश्यक है। ये पाँच भाग निम्न प्रकार हैं:
(i) जब चार भुजाएँ और एक विकर्ण दिया हो।
(ii) जब दो विकर्ण और तीन भुजाएँ दी गई हों।
(iii) दो आसन्न भुजाएँ तथा तीन कोण दिए गए हो।
(iv) जब तीन भुजाएँ तथा इनके दो कोण दिए गए हों।
क्या आप एक समांतर चतुर्भुज BATS की रचना कर सकते हैं जिसमें BA = 5cm, AT = 6 cm और AS = 6.5 cm हो? क्यों?
हाँ, समांतर चतुर्भुज BATS को दिए आँकड़ों के साथ बना सकते हैं, क्योंकि आसानी से दो ![]() और
और ![]() बना सकते हैं।
बना सकते हैं।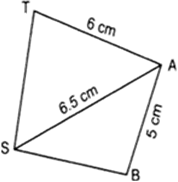
क्या आप एक सम चतुर्भुज (Rhombus) ZEAL की रचना कर सकते हैं जिसमें ZE = 3.5 cm, विकर्ण EL = 5 cm हैं? क्यों?
हाँ, दिए गए आँकड़ों द्वारा सम चतुर्भुज खींच सकते हैं, क्योंकि ये आसानी से बनने वाले दो ![]() और
और ![]() बना सकते हैं ।
बना सकते हैं ।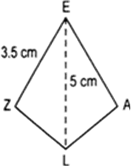
Sponsor Area
Mock Test Series
Mock Test Series





