Sponsor Area
चतुर्भुजों को समझना
निम्नलिखित प्रत्येक में कितने विकर्ण हैं?
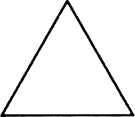
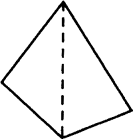
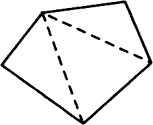
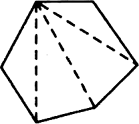
(a) एक उत्तल चतुर्भुज (b) एक समषड्भुज (c) एक त्रिभुज
![]()
(a) एक उत्तल चतुर्भुज में भुजाओं की संख्या (n) = 4
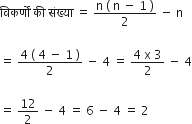
(b) एक समषड्भुज में भिजाओं की संख्या (n) = 6
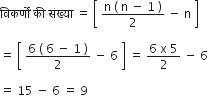
(c) एक त्रिभुज में भुजाओं की संख्या (n) = 3
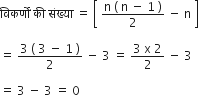
उत्तल चतुर्भुज के कोणों की मापों का युगफल क्या है? यदि चतुर्भुज, उत्तल न हो तो क्या यह गुण लागू होगा? ( एक चतुर्भुज बनाइए जो उत्तल न हो और प्रयास कीजिए।)
उत्तल चतुर्भुज के कोणों की मापों का योग 3600 होता है।
हाँ, यदि चतुर्भुज उत्तल न हो तो भी यह गुण लागू होगा।
तालिका की जाँच कीजिए: ( प्रत्येक आकृति को त्रिभुजों में बाँटिए और कोणों का योगफल ज्ञात कीजिए )
|
आकृति |
|
|
|
|
|
भुजा |
3 |
4 |
5 |
6 |
|
कोणों का योगफल |
180° |
2 x 180° = (4 - 2) x 180° |
3 x 180° = (5 - 2) x 180° |
4 x 180° = (6 - 2) x 180° |
एक बहुभुज के कोणों के बारे में आप क्या कह सकते हैं जिसकी भुजाओं की संख्या निम्नलिखित हो?
(a) 7 (b) 8 (c) 10 (d) n
ऊपर दी गई तालिका में यह स्पष्ट है कि n भुजाओं वाले बहुभुज के कोणों ( अंत:कोणों ) का योग = (n - 2) x 180°
(a) जब n = 7
= (n - 2) x 180° = (7 - 2) x 180°
= 5 x 180°
= 900°
(b) जब n = 8
= (n - 2) x 180° = (8 - 2) x 180°
= 6 x 180°
= 1080°
(c) जब n = 10
= (n - 2) x 180° = (10 - 2) x 180°
= 8 x 180°
= 1440°
(d) जब n = n
= (n - 2) x 180°
सम बहुभुज क्या है?
एक सम बहुभुज का नाम बताइए जिसमें
(i) 3 भुजाएँ (ii) 4 भुजाएँ (iii) 5 भुजाएँ हों।
एक बहुभुज को सम बहुभुज कहते हैं, क्यादि इसके सभी
(i) अंत:कोण बराबर हों, (ii) भुजाएँ बराबर हों और (iii) बाह्य कोण बराबर हों।
सम बहुभुज जिनकी
(i) 3 भुजाएँ हैं, समबाहु त्रिभुज कहलाता है।
(ii) 4 भुजाएँ हैं, वर्ग कहलाता है।
(iii) 6 भुजाएँ हैं, सम षड्भुज कहलाता है।
Sponsor Area
Mock Test Series
Mock Test Series