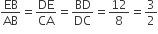7.6 cm लंबा एक रेखाखंड खींचिए और इसे 5:8 अनुपात में विभाजित कीजिए। दोनों भागों को मापिए।
रचना के चरण:
(i) पैमाने की सहायता से 7.6cm लंबा एक रेखाखंड AB खींचिए।
(ii) AB से एक न्यून कोण बनाती हुई किरण AX खींचिए।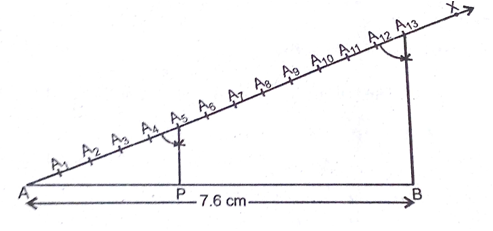
(iii) किरण AX पर 13(5+8) बिंदु A1, A2, A3, A4, A5, A6, A7, A8, A9, A10, A11, A12 और A13 इस प्रकार अंकित कीजिए कि AA1 = A1A2 = A2A3 = A3A4= A4A5 = A5A6 = A6A7 = A7A8 = A8A9 = A9A10 = A10A11 = A11A12=A12A13 हो।
(iv) A13B को मिलाइए।
(v) A5 से A5P || A13B खींचने के लिए बिंदु A5 पर  बनाइए।
बनाइए।
(vi) इस प्रकार प्राप्त बिंदु P अभीष्ट बिंदु है जो AB को 5:8 के अनुपात में विभाजित करता है।
(vii) पैमाने के सहायता से दोनों भागों को मापने पर AP = 2.9 cm तथा PB = 4.7cm (लगभग) प्राप्त होते हैं।
प्रतिपादन - त्रिभुज ABA13 में A5P || A13B है।
अत: आधारभूत समानुपातिका प्रमेय से,
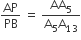
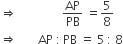






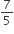 गुनी हों।
गुनी हों। प्राप्त कीजिए।
प्राप्त कीजिए।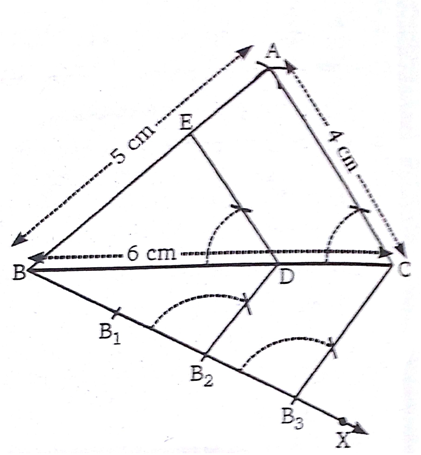
 बनाइए तथा B2D को मिलाइए।
बनाइए तथा B2D को मिलाइए। बनाइए जो AB को E पर काटे।
बनाइए जो AB को E पर काटे। की भुजाओं की
की भुजाओं की  गुनी है।
गुनी है। में
में  है।
है।
 (AAA समरूपता से)
(AAA समरूपता से)
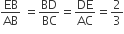
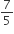 गुनी हों।
गुनी हों। 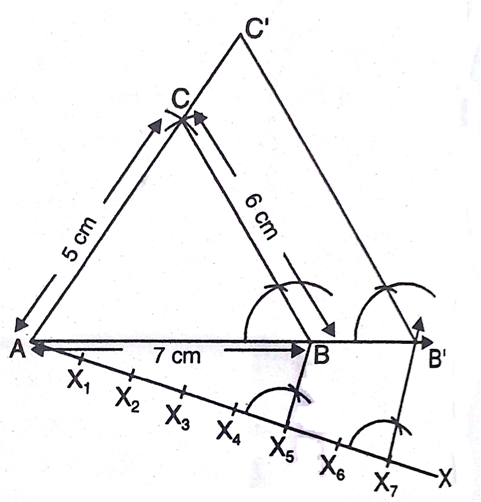
 अभीष्ट त्रिभुज है जिसकी भुजाएँ
अभीष्ट त्रिभुज है जिसकी भुजाएँ  की भुजाओं का
की भुजाओं का 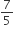 वां भाग हैं।
वां भाग हैं। में BC || B'C' है।
में BC || B'C' है।
 (AAA समरूपता से)
(AAA समरूपता से)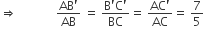
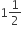 गुनी हों।
गुनी हों।  प्राप्त कीजिए।
प्राप्त कीजिए।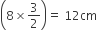
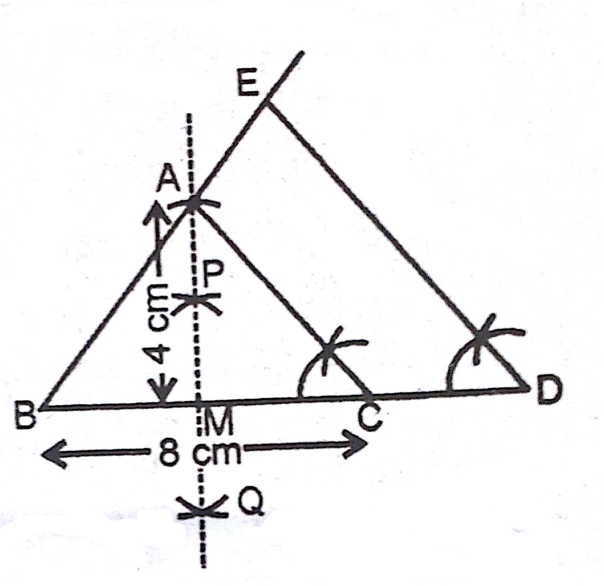
 बनाइए जो BA को बढ़ाने पर E पर मिले।
बनाइए जो BA को बढ़ाने पर E पर मिले। 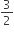 गुना है।
गुना है।  में AC||DE है।
में AC||DE है। 
 (AAA समरूपता से)
(AAA समरूपता से)