Sponsor Area
वास्तविक संख्याएँ
निम्नलिखित संख्याओं का HCF ज्ञात करने के लिए यूक्लिड विभाजन का प्रयोग कीजिए:
(i)135 और 225 (ii) 196 और 38220 (iii) 867 और 255
(i) बड़े पूर्णांक से शुरू कीजिए अर्थात 225 विभाजन एल्गोरिथम का प्रयोग करते हुए हम प्राप्त करते हैं:![]()
अब 135 को भाज्य और 90 को भाजक मानकर दोबारा विभाजन एल्गोरिथम का प्रयोग करते हुए हम प्राप्त करते हैं:![]()
अब 90 को भाज्य और 45 को भाजक मानकर एक बार फिर विभाजन एल्गोरिथम का प्रयोग करते हुए हम प्राप्त करते हैं:![]()
अब शेषफल 0 प्राप्त हुआ है इसलिए हमारी प्रक्रिया समाप्त हुई
135 और 225 का HCF 45 हैl
(ii) अब 38220 को भाज्य और 196 को भाजक मानकर दोबारा विभाजन एल्गोरिथम का प्रयोग करते हुए हम प्राप्त करते हैं:![]()
अब शेषफल 0 प्राप्त हुआ है इसलिए हमारी प्रक्रिया समाप्त हुई
इसलिए 196 और 38220 का HCF 196 हैl
(iii) 867 = 255 x 3 + 102
255 = 102 x 2 + 51
102 = 51 x 2 + 0
अब शेष '0' रह गया है, इसलिए हमारी प्रक्रिया समाप्त हुई और
HCF (867, 255) = 51
जाँच: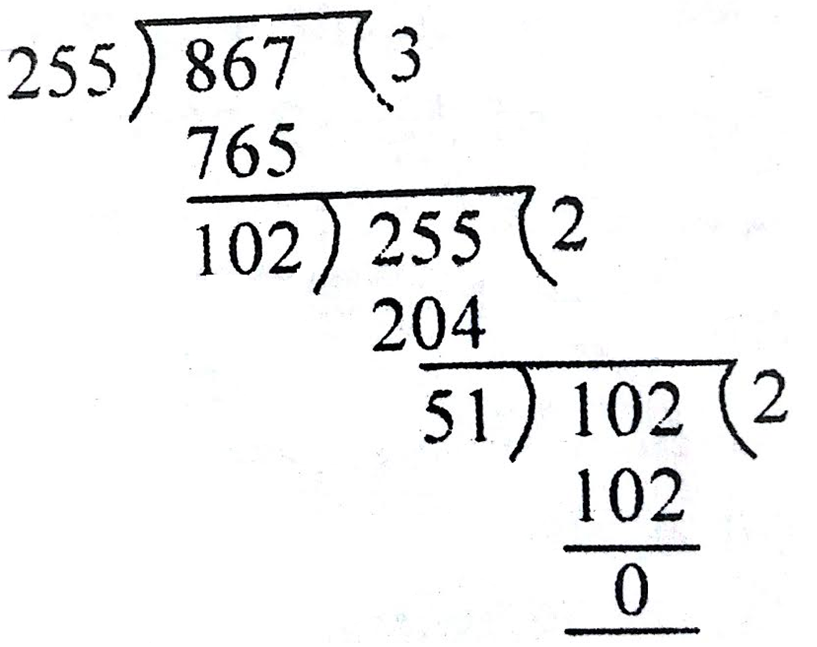
दर्शाइए कि कोई भी धनात्मक विषम पूर्णांक 6q + 1 या 6q + 3 या 6q + 5 के रूप का होता है, जहाँ 'q' कोई पूर्णांक हैl
माना a कोई धनात्मक पूर्णांक है, और b = 6
माना q भागफल है और r शेषफल हैl
विभाजन अल्गोरिथम का प्रयोग करने पर
हमें प्राप्त होता है:

किसी परेड में 616 सदस्यों वाली एक सेना ( आर्मी ) की टुकड़ी को 32 सदस्यों वाले एक आर्मी बैंड के पीछे मार्च करना हैl दोनों समूहों को समान संख्या वाले स्तंभो में मार्च करना हैl उन स्तंभों की अधिकतम संख्या क्या है जिसमें वह मार्च कर सकते हैं?
सेना की टुकड़ी में सदस्यों की संख्या = 616
आर्मी बैंड में सदस्यों की संख्या = 32
32 और 616 का यूक्लिड विभाजन के साथ HCF निकलने पर
हमें प्राप्त होता है![]()
![]()
अब भागफल 0 हैl
इसलिए स्तंभों की संख्या 8 होगी
यूक्लिड विभाजन प्रमेयिका का प्रयोग करके दर्शाइए कि किसी धनात्मक पूर्णाक का वर्ग, किसी पूर्णांक m के लिए 3m या 3m + 1 के रूप का होता हैl
[ संकेत: यह मान लीजिए x कोई धनात्मक पूर्णांक हैl तब, यह 3q, 3q+ 1, या 3q + 2 के लिखा जा सकता हैl इन में से प्रत्येक का वर्ग कीजिए और दर्शाइए कि इन वर्गों को 3m या 3m + 1 के रूप में लिखा जा सकता हैl ]
माना a कोई धनात्मक पूर्णांक है, q भागफल है, r शेषफल है
तब a = bq + r जहाँ q और r भी धनात्मक पूर्णांक है और 0 ≤ r < b
b = 3, हमें प्राप्त होता है
a = 3q + r; जहाँ 0 ≤ r < 3
जब, r = 0 = ⇒ a = 3q
जब, r = 1 = ⇒ a = 3q + 1
जब, r = 2 = ⇒ a = 3q + 2
अब हम यह दर्शाएगें की धनात्मक पूर्णांक का वर्ग 3q, 3q + 1 और 3q + 2 की तरह से लिखा जा सकता है 3m or 3m + 1 किसी m पूर्णांक के लिए
⇒ 3q = (3q)2
= 9q2 = 3(3q2) = 3 m जहाँ m कोई पूर्णांक हैl
3q + 1 = (3q + 1)2
= 9q2 + 6q + 1 = 3(3q2 + 2 q) + 1
= 3m +1, जहाँ m कोई पूर्णांक हैl
3q + 2 = (3q + 2)2
= (3q + 2)2
= 9q2 + 12q + 4
= 9q2 + 12q + 3 + 1
= 3(3q2 + 4q + 1)+ 1
= 3m + 1 किसी m पूर्णांक के लिए
∴ किसी धनात्मक पूर्णांक का वर्ग या तो 3m या 3m + 1 के रूप में होता हैl
Sponsor Area
Mock Test Series
Mock Test Series





