Sponsor Area
पृष्ठीय क्षेत्रफल और आयतन
दो घनों, जिनमें से प्रत्येक का आयतन 64 cm3 है, के सलंग्न फलकों को मिलाकर एक ठोस बनाया जाता है। इससे प्राप्त घनाभ का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
माना दिए गए प्रत्येक घन की भुजा = a cm
प्रश्नानुसार,
दिए गए प्रत्येक घन का आयतन = 64 cm3
a = 4
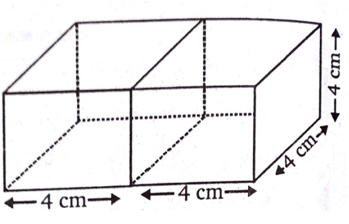
अब दो घनों को मिलाकर रखने से बने घनाभ के लिए
लंबाई(l) = (4+4)cm = 8 cm
चौड़ाई (b) = 4 cm
ऊँचाई (h) = 4 cm
∴ घनाभ का पृष्ठीय क्षेत्रफल = 2 (lb + bh + hl)
= 2(8 x 4 + 4 x 4 + 4 x 8)cm2
= 2(32+16+32)cm2
= 2 x 80 cm2 = 160 cm2
कोई बर्तन एक खोखले अर्धगोले के आकर का है जिसके ऊपर एक खोखला बेलन अध्यारोपित है। अर्धगोले का व्यास 14cm है और इस बर्तन (पात्र) की कुल ऊँचाई 13cm है। इस बर्तन का आंतरिक पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
यहाँ पर, बर्तन के अर्धगोले का व्यास = 14 cm
बर्तन के अर्धगोले की त्रिज्या (r) =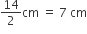 
बर्तन के अर्धगोले का पृष्ठीय क्षेत्रफल = 
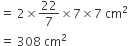
बर्तन के बेलनाकार भाग की त्रिज्या (r) =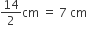 
बर्तन के बेलनाकार भाग की ऊँचाई (h) = (13 - 7)cm = 6 cm
बर्तन के बेलनाकार भाग का वक्र पृष्ठीय क्षेत्रफल = 
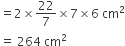
अत: बर्तन का आंतरिक पृष्ठीय क्षेत्रफल = (308 + 264) cm2
= 572 cm2
एक खिलौना त्रिज्या 3.5 cm वाले एक शंकु के आकर का हो, जो उसी त्रिज्या वाले एक अर्धगोले पर अध्यारोपित है। इस खिलौने की सम्पूर्ण ऊँचाई 15.5 cm है। इस खिलौने का संपूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
यहाँ पर,
खिलौने के अर्धगोलाकार भाग की त्रिज्या (r) = 3.5 cm
खिलौने के अर्धगोलाकार भाग का पृष्ठीय क्षेत्रफल = 
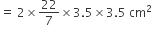
= 77 cm2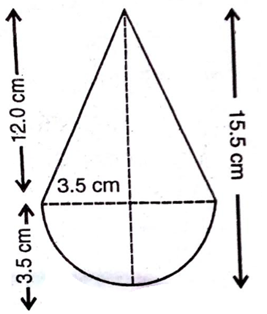
खिलौने के शंकु वाले भाग की त्रिज्या (r) = 3.5 cm
खिलौने के शंकु वाले भाग की ऊँचाई (h) = (15.5 - 3.5)cm = 12 cm
खिलौने के शंकु वाले भाग की तिर्यक ऊँचाई (l) =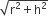 
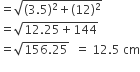
खिलौने के शंकु वाले भाग का पृष्ठीय क्षेत्रफल = 
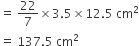
अत: खिलौने का संपूर्ण पृष्ठीय क्षेत्रफल = (अर्धगोलाकार + शंकु वाले भाग का पृष्ठीय क्षेत्रफल)
= (77+137.5)cm2 = 214.5 cm2
भुजा 7cm वाले एक घनाकार ब्लॉक के ऊपर एक अर्धगोला रखा हुआ है। अर्धगोले का अधिकतम व्यास क्या हो सकता है? इस प्रकार बने ठोस का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
यहाँ पर, घनाकार ब्लॉक की भुजा = 7 cm
प्रश्नानुसार अर्धगोले का अधिकतम व्यास = घनाकार ब्लॉक की भुजा 
अर्धगोले का अधिकतम व्यास = 7 cm
अर्धगोले की त्रिज्या (r) = 
घनाकार ब्लॉक का पृष्ठीय क्षेत्रफल = 6(भुजा)2
= 6 x 7 x 7 cm2
= 294 cm2
अर्धगोले का पृष्ठीय क्षेत्रफल =
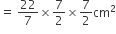
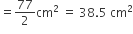
अत: पूर्ण ठोस का पृष्ठीय क्षेत्रफल = (294 + 38.5) cm2
= 332.5 cm2
Sponsor Area
Mock Test Series
Mock Test Series