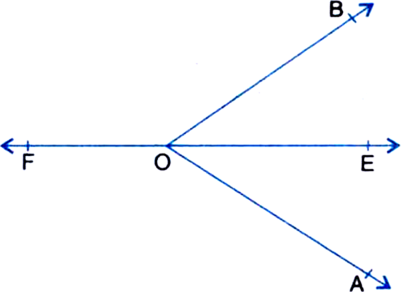
∠FOB + ∠BOE = 180° ...(1)
| Linear Pair Axiom
∠FOA + ∠AOE = 180° ...(2)
| Linear Pair Axiom
From (1) and (2),
∠FOB + ∠BOE = ∠FOA + ∠AOE ...(3)
But    ∠BOE = ∠AOE
| ∵ Ray OE bisects ∠AOB
∴ From (3),
⇒    ∠FOB = ∠FOA.

Construction. Draw a ray OP opposite to ray OA.
Proof. ∠AOB + ∠BOC + ∠COP = 180° ...(1)
| ∵ A straight angle = 180°
∠POD + ∠DOE + ∠EOA = 180° ...(2)
| ∵ A straight angle = 180°
Adding (1) and (2), we get
∠AOB + ∠BOC + (∠COP + ∠POD) + ∠DOE + ∠EOA = 180° + 180° = 360°
⇒ ∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOA = 360°.
 

Let AB and CD be two lines intersecting at O.

This leads to two pairs of vertically opposite angles, namely,
(i) ∠AOC and ∠BOD
(ii) ∠AOD and ∠BOC
We are to prove that
(i) ∠AOC = ∠BOD
and (ii) ∠AOD = ∠BOC
∵ Ray OA stands on line CD Therefore,
∠AOC + ∠AOD = 180°    ...(1)
| Linear Pair Axiom
∵ Ray OD stands on line AB Therefore,
∠AOD + ∠BOD = 180°    ...(2)
| Linear Pair Axiom
From (1) and (2),
∠AOC + ∠AOD = ∠AOD + ∠BOD
⇒    ∠AOC = ∠BOD
Similarly, we can prove that
∠AOD = ∠BOC

Given: OP bisects ∠AOC, OQ bisects ∠BOC and OP ⊥ OQ.
To Prove: The points A, O and B are collinear.
Proof: ∵ OP bisects ∠AOC
∴ ∠AOP = ∠COP    ...(1)
∵ OQ bisects ∠BOC
∠BOQ = ∠COQ    ...(2)
Now, ∠AOB
= ∠AOP + ∠COP + ∠COQ + ∠BOQ
= ∠COP + ∠COP + ∠COQ + ∠COQ
| From (1) and (2)
= 2(∠COP + ∠COQ)
= 2 ∠POQ
= 2(90°)    | ∵ OP ⊥ OQ
= 180°
∴ The points A, O and B are collinear.
| By converse of Linear Pair Axiom