Let ABCD be a quadrilateral in which
∠A : ∠B : ∠C : ∠D = 3 : 5 : 9 : 13
Sum of the ratios = 3 + 5 + 9+ 13 = 30
Also, ∠A + ∠B + ∠C + ∠D = 360°
Sum of all the angles of a quadrilateral is 360°

Given: In parallelogram ABCD, AC = BD.
To Prove: ||gm ABCD is a rectangle.

Proof: In ∆ACB and ∆BDA,
AC = BD    | Given
AB = BA    | Common
BC = AD
| Opposite sides of || gm ABCD
∴ ∆ACB ≅ ∆BDA
| SSS Congruence Rule
∴ ∠ABC = ∠BAD ...(1) C.P.C.T.
Again, ∵ AD || BC
| Opp. sides of || gm ABCD and transversal AB intersects them.
∴ ∠BAD + ∠ABC = 180°    ...(2)
| Sum of consecutive interior angles on the same side of a transversal is 180°
From (1) and (2),
∠BAD = ∠ABC = 90°
∴ ∠A = 90°
∴ || gm ABCD is a rectangle.

Given: ABCD is a quadrilateral whose diagonals AC and BD intersect each other at right angles at O.
To Prove: Quadrilateral ABCD is a rhombus.

Proof: In ∆AOB and ∆AOD,
AO = AO    | Common
OB = OD    | Given
∠AOB = ∠AOD    | Each = 90°
∴ ∆AOB ≅ ∆AOD
| SSS Congruence Rule
∴ AB = AD    ...(1) | C.P.C.T.
Similarly, we can prove that
AB = BC    ...(2)
BC = CD    ...(3)
CD = AD    ...(4)
In view of (1), (2), (3) and (4), we obtain
AB = BC = CD = DA
∴ Quadrilateral ABCD is a rhombus.

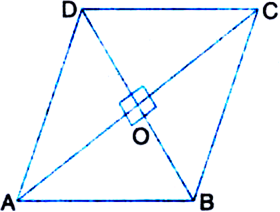
Given: ABCD is a square.
To Prove: (i) AC = BD
(ii) AC and BD bisect each other at right angles.
Proof: (i) In ∆ABC and ∆BAD,

AB = BA    | Common
BC = AD    Opp. sides of square ABCD
∠ABC = ∠BAD | Each = 90°
(∵ ABCD is a square)
∴ ∆ABC ≅ ∆BAD
| SAS Congruence Rule
∴ AC = BD    | C.P.C.T
(ii) In ∆OAD and ∆OCB,
AD = CB
| Opp. sides of square ABCD
∠OAD = ∠OCB
| ∵    AD || BC and transversal AC intersects them
∠ODA = ∠OBC
| ∵    AD || BC and transversal BD intersects them
∴ ∆OAD ≅ ∆OCB
| ASA Congruence Rule
∴ OA = OC    ...(1)
Similarly, we can prove that
OB = OD    ...(2)
In view of (1) and (2),
AC and BD bisect each other.
Again, in ∆OBA and ∆ODA,
OB = OD | From (2) above
BA = DA
| Opp. sides of square ABCD
OA = OA    | Common
∴ ∆OBA ≅ ∆ODA
| SSS Congruence Rule
∴ ∠AOB = ∠AOD    | C.P.C.T.
But ∠AOB + ∠AOD = 180°
| Linear Pair Axiom
∴ ∠AOB = ∠AOD = 90°
∴ AC and BD bisect each other at right angles.