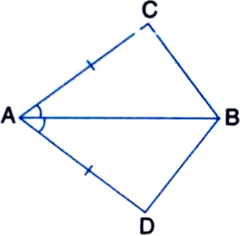
Given: In quadrilateral ACBD, AC = AD and AB bisects ∠A.
To Prove: ∆ABC ≅ ∆ABD.
Proof: In ∆ABC and ∆ABD,
AC = AD    | Given
AB = AB    | Common
∠CAB = ∠DAB
| ∵ AB bisects ∠A
∴ ∠ABC ≅ ∠ABD    | SAS Rule
∴ BC = BD    | C.P.C.T,

Given: ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA.
To Prove: (i) ∆ABD ≅ ∆BAC
(ii)    BD = AC
(iii)    ∠ABD = ∠BAC.
Proof: (i) In ∆ABD and ∆BAC,
AD = BC    | Given
AB = BA    | Common
∠DAB = ∠CBA    | Given
∴ ∆ABD ≅ ∠BAC    | SAS Rule
(ii)    ∵ ∆ABD ≅ ∆BAC    | Proved in (i)
∴ BD = AC    | C.P.C.T.
(iii)    ∵ ∆ABD ≅ ∠BAC    | Proved in (i)
∴ ∠ABD = ∠BAC.    | C.P.C.T.

Given: AD and BC are equal perpendiculars to a line segment AB.
To Prove: CD bisects AB.
Proof: In ∆O AD and ∆OBC
AD = BC    | Given
∠OAD = ∠OBC    | Each = 90°
∠AOD = ∠BOC
| Vertically Opposite Angles
∴ ∠OAD ≅ ∆OBC    | AAS Rule
∴ OA = OB    | C.P.C.T.
∴ CD bisects AB.

Given: I and m are two parallel lines intersected by another pair of parallel lines p and q.
To Prove: ∆ABC ≅ ∆CDA.
Proof: ∵ AB || DC
and    AD || BC
∴ Quadrilateral ABCD is a parallelogram.
| ∵ A quadrilateral is a parallelogram if both the pairs of opposite sides are parallel
∴ BC = AD    ...(1)
| Opposite sides of a ||gm are equal
AB = CD    ...(2)
| Opposite sides of a ||gm are equal
and ∠ABC = ∠CDA    ...(3)
| Opposite angles of a ||gm are equal
In ∆ABC and ∆CDA,
AB = CD    | From (2)
BC = DA    | From (1)
∠ABC = ∠CDA    | From (3)
∴ ∆ABC ≅ ∆CDA.    | SAS Rule