Sponsor Area
The Triangle and its Properties
In ΔPQR, D is the mid-point of .
is __________.
PD is __________.
Is QM = MR?
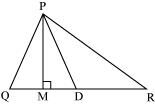
(i) Altitude
(ii) Median
(iii) No
Draw rough sketches for the following:
(a) In ΔABC, BE is a median.
(b) In ΔPQR, PQ and PR are altitudes of the triangle.
(c) In ΔXYZ, YL is an altitude in the exterior of the triangle
(a)

(b)

(c)

Here, it can be observed that for ΔXYZ, YL is an altitude drawn exterior to side XZ which is extended up to point L.
Verify by drawing a diagram if the median and altitude of an isosceles triangle can be same.
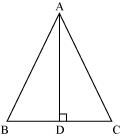
Draw a line segment AD perpendicular to BC. It is an altitude for this triangle. It can be observed that the length of BD and DC is also same. Therefore, AD is also a median of this triangle.
Find the value of the unknown exterior angle x in the following diagrams:
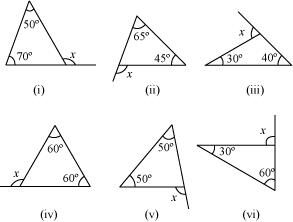
(i) x = 50° + 70° (Exterior angle theorem)
x = 120°
(ii) x = 65° + 45° (Exterior angle theorem)
= 110°
(iii) x = 40° + 30° (Exterior angle theorem)
= 70°
(iv) x = 60° + 60° (Exterior angle theorem)
= 120°
(v) x = 50° + 50° (Exterior angle theorem)
= 100°
(vi) x = 30° + 60° (Exterior angle theorem)
= 90°
Sponsor Area
Mock Test Series
Mock Test Series





