Sponsor Area
Practical Geometry
Draw a line, say AB, take a point C outside it. Through C, draw a line parallel to AB using ruler and compasses only.
The steps of construction are as follows.
(i)Draw a line AB. Take a point P on it. Take a point C outside this line. Join C to P.
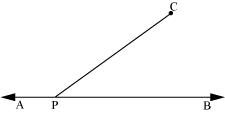
(ii)Taking P as centre and with a convenient radius, draw an arc intersecting line AB at point D and PC at point E.
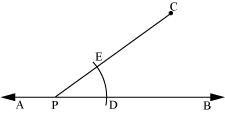
(iii) Taking C as centre and with the same radius as before, draw an arc FG intersecting PC at H.
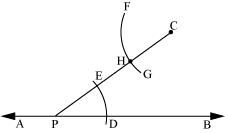
(iv) Adjust the compasses up to the length of DE. Without changing the opening of compasses and taking H as the centre, draw an arc to intersect the previously drawn arc FG at point I.
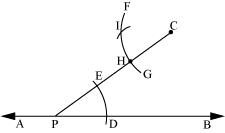
(v) Join the points C and I to draw a line ‘l’.
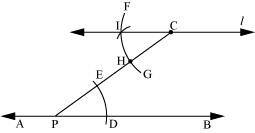
This is the required line which is parallel to line AB.
Draw a line l. Draw a perpendicular to l at any point on l. On this perpendicular choose a point X, 4 cm away from l. Through X, draw a line m parallel to l.
The steps of construction are as follows.
(i) Draw a line l and take a point P on line l. Then, draw a perpendicular at point P.

(ii) Adjusting the compasses up to the length of 4 cm, draw an arc to intersect this perpendicular at point X. Choose any point Y on line l. Join X to Y.

(iii) Taking Y as centre and with a convenient radius, draw an arc intersecting l at A and XY at B.

(iv) Taking X as centre and with the same radius as before, draw an arc CD cutting XY at E.

(v)Adjust the compasses up to the length of AB. Without changing the opening of compasses and taking E as the centre, draw an arc to intersect the previously drawn arc CD at point F.

(vi) Join the points X and F to draw a line m.

Line m is the required line which is parallel to line l.
Let l be a line and P be a point not on l. Through P, draw a line m parallel to l. Now join P to any point Q on l. Choose any other point R on m. Through R, draw a line parallel to PQ. Let this meet l at S. What shape do the two sets of parallel lines enclose?
The steps of construction are as follows.
(i)Draw a line l and take a point A on it. Take a point P not on l and join A to P.

(ii) Taking A as centre and with a convenient radius, draw an arc cutting l at B and AP at C.

(iii)Taking P as centre and with the same radius as before, draw an arc DE to intersect AP at F.

(iv) Adjust the compasses up to the length of BC. Without changing the opening of compasses and taking F as the centre, draw an arc to intersect the previously drawn arc DE at point G.

(v)Join P to G to draw a line m. Line m will be parallel to line l.

(vi)Join P to any point Q on line l. Choose another point R on line m. Similarly, a line can be drawn through point R and parallel to PQ.

Let it meet line l at point S.
In quadrilateral PQSR, opposite lines are parallel to each other.
PQ || RS and PR || QS
Thus, the quadrilateral PQSR is a parallelogram.
Construct ΔXYZ in which XY = 4.5 cm, YZ = 5 cm and ZX = 6 cm.
The rough figure of this triangle is as follows.
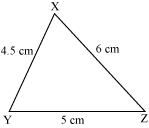
The required triangle is constructed as follows.
(i) Draw a line segment YZ of length 5 cm.
![]()
(ii) Point X is at a distance of 4.5 cm from point Y. Therefore, taking point Y as centre, draw an arc of 4.5 cm radius.
(iii) Point X is at a distance of 6 cm from point Z. Therefore, taking point Z as centre, draw an arc of 6 cm radius. Mark the point of intersection of the arcs as X. Join XY and XZ.
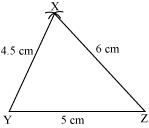
XYZ is the required triangle.
Sponsor Area
Mock Test Series
Mock Test Series





