Sponsor Area
Wave Optics
A small candle, 2.5 cm in size is placed at 27 cm in front of a concave mirror of radius of curvature 36 cm. At what distance from the mirror should a screen be placed in order to obtain a sharp image? Describe the nature and size of the image. If the candle is moved closer to the mirror, how would the screen have to be moved?
Given,
Object size = 2.5 cm
The negative sign indicates that the image is formed in front of the mirror. Thus, the screen should be placed at a distance of 54 cm in front of the mirror on the same side as that of the object.
Now,
Magnification,
As size of image is (–)ve. So image is inverted and real.
When the candle is moved closer to mirror, the screen would have to be moved farther and farther. However, when the candle is closer than 18 cm from the mirror, the image would be virtual and therefore cannot be collected on the screen.
A 4.5 cm needle is placed 12 cm away from a convex mirror of focal length 15 cm. Give the location of the image and the magnification. Describe what happens as the needle is moved farther from the mirror.
Given,
Now using the mirror formula,
we have,
∴ Image is formed at 6.7 cm at the back of the mirror ( because v is positive)
Now,
Magnification,
Hence, the image formed is erect, and of course virtual.
As, needle is moved farther away from the mirror then as a result, image moves away from the mirror (upto F) and keeps on decreasing in size.
A tank is filled with water to a height of 12.5 cm. The apparent depth of a needle lying at the bottom of the tank is measured by a microscope to be 9.4 cm. What is the refractive index of water? If water is replaced by a liquid of refractive index 1.63 up to the same height, by what distance would the mircoscope have to be moved to focus on the needle again?
Case I: When tank is filled with water.
Given, real depth = 12.5 cm;
apparent depth = 9.4 cm
Now, using the formula,
we have,
Refractive index,
Case II: When water in the tank is replaced by another liquid.
Therefore,
i.e.,
Distance through which microscope has to be moved downward is = (9.4 – 7.67) cm = 1.73 cm.
Figures (a) and (b) show refraction of a ray in air incident at 60° with the normal to a glass-air and water-air interface, respectively. Predict the angle of refraction in glass when the angle of incidence in water is 45° with the normal to a water-glass interface. [ Fig. 9.34 (c)].
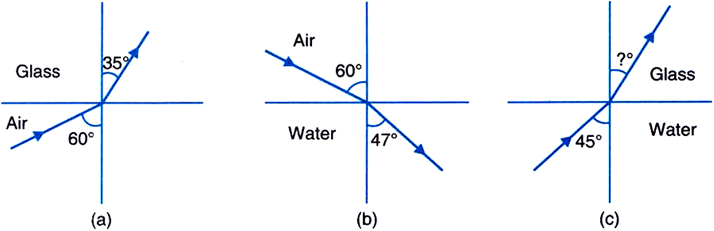
(a)
Given,
Using Snell's law, we have
Refractive index of glass with respect to air,
(b)
Using Snell's law,
Refractive index of water wr.to air,
(c)
Angle of incidence in water,
Refractive index of glass wr.to water,
Sponsor Area
Mock Test Series
Mock Test Series





