Sponsor Area
Sets
Use principle of mathematical induction to prove that:![]()
Let P(n): 1 + 2 + 3 + ......... + n = ![]()
I. For n = 1,
P(1) : 1 = ![]() is true.
is true.
II. Suppose the statement is true for n = m, ![]()
i.e. P(m): ![]() ....(i)
....(i)
III. For n = m + 1,
P(m + 1): 1 + 2 + 3 + ........ + (m + 1) = ![]()
or [1 + 2 + 3 + ...... + m] + (m + 1) = ![]()
[From (i), 1 + 2 + 3 + ...... + m = ![]() ]
]
∴ P (m + 1): ![]()
![]()
![]()
![]()
![]()
![]()
![]()
which is true
∴ P(m + 1) is true
∴ P(m) is true ![]() P(m + 1) is true
P(m + 1) is true
Hence, by mathematical induction
P(n) is true for all ![]()
Prove the following by using the principle of mathematical induction for all ![]()
![]()
Let ![]()
I. For n = 1,
![]() is true.
is true.
II. Suppose the statement is true for n = m, ![]()
i.e.,  ... (i)
... (i)
III. For n = m + 1,
![]()
or ![]()
From (i), ![]()
∴ ![]()
![]()
![]()
![]()
which is true
∴ P(m + 1) is true
∴ P(m) is true ![]() P(m + 1) is true.
P(m + 1) is true.
Hence, by mathematical induction, P(n) is true for all ![]()
Prove the following by using the principle of mathematical induction for all ![]() :
:![]()
Let P(n) : ![]()
I. For n = 1,
P(1) : 1 ![]()
∴ P(1) is true.
II. Let the statement be true for n = m, ![]()
∴ P(m) : ![]() ... (i)
... (i)
III. For n = m + 1,
P(m + 1) : ![]()
or ![]()
From (i), ![]()
∴ ![]()
![]()
which is true.
∴ P(m + 1) is true.
∴ P(m) is true ![]() P (m + 1) is true
P (m + 1) is true
Hence, by principle of mathematical induction, P(n) is true for all ![]()
Prove the following by using the principle of mathematical induction for all ![]() :
:![]()
Let P(n): ![]()
I. For n = 1,
P(1) : ![]()
∴ P(1) is true.
II. Let the statement be true
for n = m, ![]()
∴ ![]() .... (i)
.... (i)
III. For n = m + 1,
P(m + 1): ![]()
or ![]()
From (i),
![]()
∴ ![]()
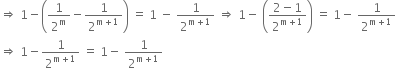
which is true.
∴ P(m + 1) is true
∴ P(m) is true ![]() P(m + 1) is true
P(m + 1) is true
Hence, by the principal of mathematical induction, P(n) is true for all ![]() .
.
Sponsor Area
Mock Test Series
Mock Test Series





