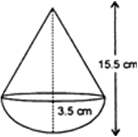
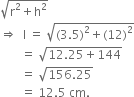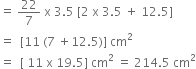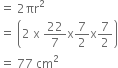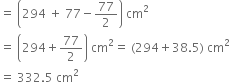2 cubes each of volume 64 cm3 are joined end to end. Find the surface area of the resulting cuboid.
Let ‘a’ be the length of a side of a cube. Then
Volume of one cube = 64 cm3
⇒ n3 = 65 cm3
⇒ n = 4 cm
On joining the cubes, a cuboid is formed.
Then The length of the resulting cuboid (l) = 2
The breadth of the resulting cuboid (b) = a cm
The thickness of the resulting cuboid (h) = a cm
Now,
Surface area of the resulting cuboid
= 2(lb + bh + hl)
= 2 (2a. a + a. a + a. 2a)
= 2 (2a2 + a2 + 2a2)
= 2 (5a2) = 10a2 = 10 (4)2
= 160 cm2.