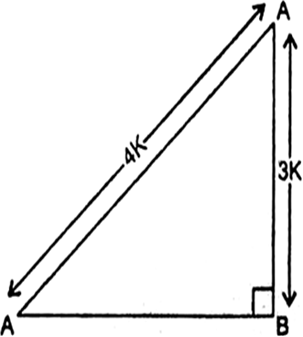
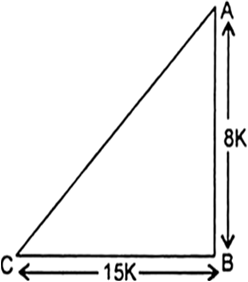
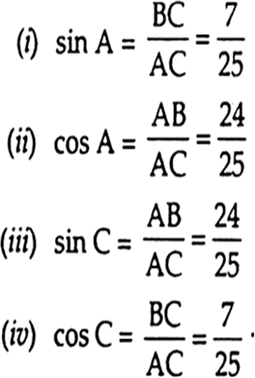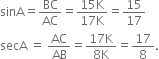In ΔABC, right angled at B. AB = 24 cm, BC = 7 cm. Determine:
(i) sin A cos A,
(ii) sin C, cos C.
Let AB = 24 cm
BC = 7cm Using Pythagoras theorem, we have
AC2 = AB2 + BC2
= (24 cm)2+ (7 cm)2
= 576 cm2 + 49 cm2
= 625 cm2
So, AC = 25 cm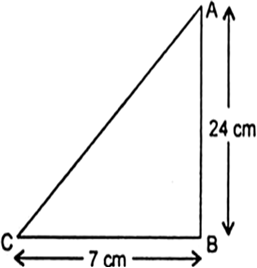
Now,