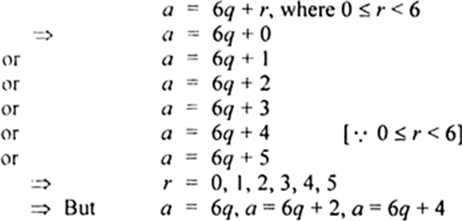Use Euclid’s division algorithm to find the HCF of:
(i)135 and 225 (ii) 196 and 38220.
(i) Given integers are 135 and 225, clearly 225 > 135. Therefore, by applying Euclid’s division lemma to 225 and 135, we get![]()
If. Since, the remaindei 90 ≠ 0, we apply division lemma to 135 and 90, to ge.![]()
We consider the new divisor 90 and new remainder 45 and apply division lemma to get![]()
The remainder of this step is zero. So, the divisor at this stage or the remainder at the previous stage i.e., 45 is the HCF of 135 and 225.
(ii) Given integers are 196 and 38220. Therefore by applying Euclid’s division lemma to 196 and 38220, we get![]()
The remainder at this step is zero. So. our procedures stops and divisor at this stage i.e. 196 is the HCF of 196 and 38220.