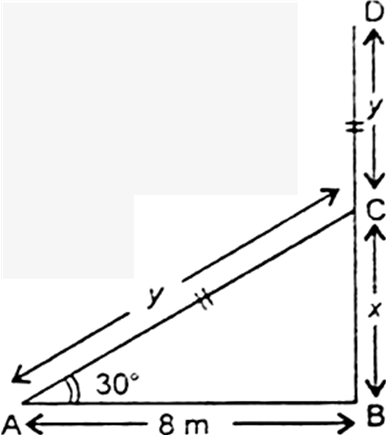
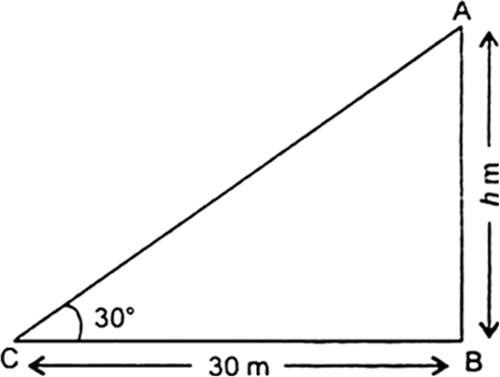
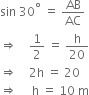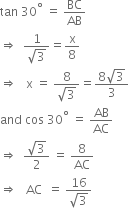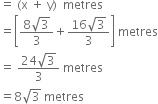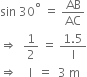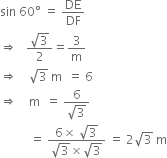A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, whereas for elder children, she wants to have a steep slide at a height of 3m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?
Solution
Short Answer
Case I :
Calculation of length of the slide below 5 years. Fig. (a)
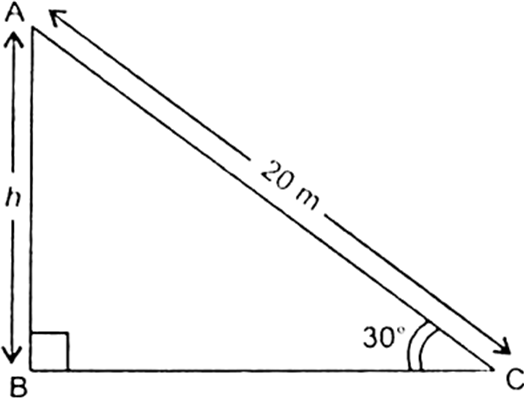
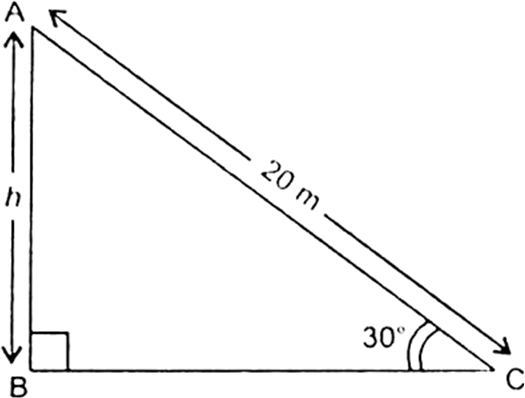
Let AC be the slide of length l m and height of the slide AB of height 1.5 m. It is given that slide is inclimed at an angle of 30°.
i.e., ∠ACB = 30°
In right triangle ABC, we have
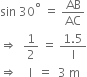
Hence, the length of the slide for below 5 years is 3 m
Case II :
Calculation of the length of slide for elder children. Fig. (b)
Let DF be the slide of length m metres and DE be the height of the top of slide of height 3 m. It is given that slide is inclined at an angle of 60°.
i.e., ∠DFE = 60°
In right triangle DEF, we have
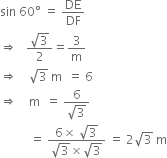
Hence, the length of the slide for elder children is