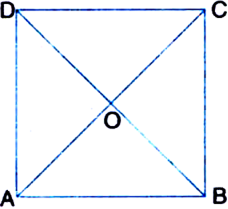
Given: ABCD is a square.
To Prove: (i) AC = BD
(ii) AC and BD bisect each other at right angles.
Proof: (i) In ∆ABC and ∆BAD,
AB = BA | Common
BC = AD Opp. sides of square ABCD
∠ABC = ∠BAD | Each = 90°
(∵ ABCD is a square)
∴ ∆ABC ≅ ∆BAD
| SAS Congruence Rule
∴ AC = BD | C.P.C.T
(ii) In ∆OAD and ∆OCB,
AD = CB
| Opp. sides of square ABCD
∠OAD = ∠OCB
| ∵ AD || BC and transversal AC intersects them
∠ODA = ∠OBC
| ∵ AD || BC and transversal BD intersects them
∴ ∆OAD ≅ ∆OCB
| ASA Congruence Rule
∴ OA = OC ...(1)
Similarly, we can prove that
OB = OD ...(2)
In view of (1) and (2),
AC and BD bisect each other.
Again, in ∆OBA and ∆ODA,
OB = OD | From (2) above
BA = DA
| Opp. sides of square ABCD
OA = OA | Common
∴ ∆OBA ≅ ∆ODA
| SSS Congruence Rule
∴ ∠AOB = ∠AOD | C.P.C.T.
But ∠AOB + ∠AOD = 180°
| Linear Pair Axiom
∴ ∠AOB = ∠AOD = 90°
∴ AC and BD bisect each other at right angles.