Sponsor Area
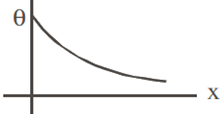
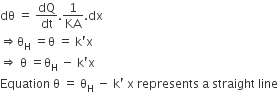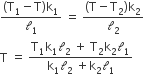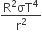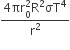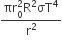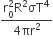A long metallic bar is carrying heat from one of its ends to the other end under steady-state. The variation of temperature θ along the length x of the bar from its hot end is best described by which of the following figure.
B.
We know that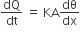 
In steady state flow of heat
Sponsor Area
One end of a thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two sections of lengths
(k2
(k2
(k1
(k1A1 T1 + k2A2T2) / (k1A1 + k2A2)
C.
(k1
If Cp and Cv denote the specific heats of nitrogen per unit mass at constant pressure and constant volume respectively, then
Cp – Cv = R/28
Cp −Cv = R/14
Cp −Cv = R
Cp – Cv = 28 R
A.
Cp – Cv = R/28
Assuming the sun to be a spherical body of radius R at a temperature of T K, evaluate the total radiant power, incident on Earth, at a distance r from the Sun.
where r0 is the radius of the Earth and σ is Stefan’s constant
C.
Sponsor Area
Mock Test Series
