Question
One ticket is selected at random from 50 tickets numbered 00, 01, 02, ... , 49. Then the probability that the sum of the digits on the selected ticket is 8, given that the product of these digits is zero, equals
-
1/14
-
1/7
-
5/14
-
1/50
Solution
A.
1/14
A = Events that sum of the digits on selected ticket is 8
= {08, 17, 26, 35, 44}
n(A) = 5
Event that product of digits is zero
= {00, 01, 02, 03, 04, 05, 06, 07, 08, 09, 10, 20,30, 40}
⇒ n(B) = 14
=P(A/B) = (5/14)
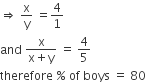
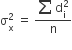(Here deviations are taken from the mean) Since A and B both have 100 consecutive integers, therefore both have same standard deviation and hence the variance. 