Sponsor Area
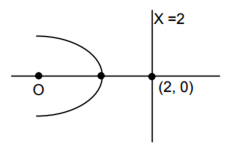
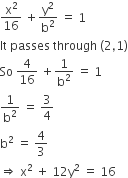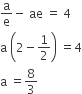The ellipse x2+ 4y2= 4 is inscribed in a rectangle aligned with the coordinate axes, which in turn is inscribed in another ellipse that passes through the point (4, 0). Then the equation of the ellipse is
x2+ 16y2= 16
x2+ 12y2= 16
4x2+ 48y2= 48
4x2+ 64y2= 48
B.
x2+ 12y2= 16
Sponsor Area
A focus of an ellipse is at the origin. The directrix is the line x = 4 and the eccentricity is 1/2. Then the length of the semi−major axis is
8/3
2/3
5/3
4/3
A.
8/3
Major axis is along x-axis.
A parabola has the origin as its focus and the line x = 2 as the directrix. Then the vertex of the parabola is at
(0, 2)
(1, 0)
(0,1)
(2,0)
B.
(1, 0)
vertex (0,1) 
Consider a family of circles which are passing through the point (-1, 1) and are tangent to x-axis. If (h, K) are the co-ordinates of the centre of the circles, then the set of values of k is given by the interva
0 < k < 1/2
k ≥ 1/2
– 1/2 ≤ k ≤ 1/2
k ≤ ½
B.
k ≥ 1/2
Equation of circle (x − h)2+ (y − k)2 = k2
It is passing through (− 1, 1) then
(− 1 − h)2+ (1 − k)2= k2
h2+ 2h − 2k + 2 = 0
D ≥ 0
2k − 1 ≥ 0 ⇒ k ≥ 1/2.
Sponsor Area
Mock Test Series
